A Collection of Quant Riddles With Answers
The quant riddles or logic or lateral puzzles 1-19 appear in the book 'Heard on The Street: Quantitative Questions from Wall Street Job Interviews' by Timothy Falcon Crack PhD available on his website, the rest have been accumulated from the internet and emails I receive. They are designed to help practice for job or university interviews or just training your brain. Realistically, in an interview you wouldn't be asked these questions and left to your own devices, you'd be prompted. That's where the clues come in, they are intended to add ideas incrementally and help you get there by yourself.. Questions 3 & 5 are probably the easiest and a good place to start. I've coloured them Red, Amber and Green to indicate the difficulty along with the bar on the right. Difficulty is very subjective, but they all offer something in teaching you the ideas and tricks used to solve them. So that's it good luck... New! I've also run the questions through ChatGPT &
Bard and (spoiler,) they did quite well!
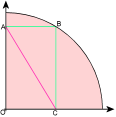 87. Quickie: Examine the diagram carefully. It shows a quadrant of a circle radius 'r', with a rectangle touching the perimeter of the circle. What is the length of the line labeled A-C.
87. Quickie: Examine the diagram carefully. It shows a quadrant of a circle radius 'r', with a rectangle touching the perimeter of the circle. What is the length of the line labeled A-C.
(click image to enlarge)
 85. A man has a rectangular garden, 55m ('B' in the diagram,) by 40m('A',) and he makes a diagonal path, 1m wide, exactly in the manner indicated in the diagram. What is the area of the path?
85. A man has a rectangular garden, 55m ('B' in the diagram,) by 40m('A',) and he makes a diagonal path, 1m wide, exactly in the manner indicated in the diagram. What is the area of the path?
(click image to enlarge)
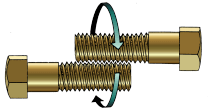 84. Two identical bolts are placed together so that their helical grooves intermesh. If you move the bolts around each other as you would twiddle your thumbs, holding each bolt firmly by the head so that it does not rotate and twiddling them in the direction shown, ill the heads a) move inward, b) move outward, or c) stay the same distance a from each other?
84. Two identical bolts are placed together so that their helical grooves intermesh. If you move the bolts around each other as you would twiddle your thumbs, holding each bolt firmly by the head so that it does not rotate and twiddling them in the direction shown, ill the heads a) move inward, b) move outward, or c) stay the same distance a from each other?
(click image to enlarge)
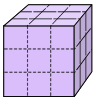 82. Quickie: A carpenter, working with a buzz saw, wishes to cut a wooden cube, three inches on each side, into 27 one-inch cubes. He can do it easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut?
82. Quickie: A carpenter, working with a buzz saw, wishes to cut a wooden cube, three inches on each side, into 27 one-inch cubes. He can do it easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut?
(click image to enlarge)
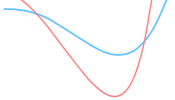 81. The diagram shows the tracks from a two wheeled bicycle. Was the bicycle traveling from left to right or right to left?
81. The diagram shows the tracks from a two wheeled bicycle. Was the bicycle traveling from left to right or right to left?
(click image to enlarge)
 78. Secret Santa is a Western Christmas tradition in which members of a group or community are randomly assigned a person to whom they anonymously give a gift.
78. Secret Santa is a Western Christmas tradition in which members of a group or community are randomly assigned a person to whom they anonymously give a gift.
The rules for determining who buys for whom are as follows. All the participants put their names in a hat. Each player will draw a name in turn. If they should draw their own name they will return it to the hat and draw another. If the last person to draw draws their own name the game is void and everyone starts again. Otherwise people will not return the name to the hat and will buy a present for the person whose name they have drawn.
Adam, Bob and Carol are to play a game of Secret Santa. They will draw in alphabetical order. What are the odds that Adam buys for Carol?
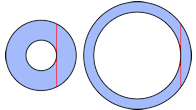 76. The diagram shows two concentric annuli (two dimensional ring shapes,) given that the two red lines are the same length, prove that the shaded areas are the same too.
76. The diagram shows two concentric annuli (two dimensional ring shapes,) given that the two red lines are the same length, prove that the shaded areas are the same too.
(click image to enlarge)
 74. There are 100 prisoners in solitary cells. There's a central living room with one light bulb; this bulb is initially off. No prisoner can see the light bulb from his or her own cell. Everyday, the warden picks a prisoner equally at random, and that prisoner visits the living room. While there, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting that all 100 prisoners have been to the living room by now. If this assertion is false, all 100 prisoners are shot. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world could always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. The prisoners are allowed to get together one night in the courtyard, to discuss a plan. What plan should they agree on, so that eventually, someone will make a correct assertion?
74. There are 100 prisoners in solitary cells. There's a central living room with one light bulb; this bulb is initially off. No prisoner can see the light bulb from his or her own cell. Everyday, the warden picks a prisoner equally at random, and that prisoner visits the living room. While there, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting that all 100 prisoners have been to the living room by now. If this assertion is false, all 100 prisoners are shot. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world could always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. The prisoners are allowed to get together one night in the courtyard, to discuss a plan. What plan should they agree on, so that eventually, someone will make a correct assertion?
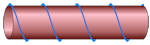 72. A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4cm and it's length is 12cm.
72. A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4cm and it's length is 12cm.
Find the length of the string.
 70. Andrew, Britney and Carol race each other in a 100 meters race. All of them run at a constant speed throughout the race.
70. Andrew, Britney and Carol race each other in a 100 meters race. All of them run at a constant speed throughout the race.
Andrew beats Britney by 20 meters.
Britney beats Carol by 20 meters.
By how many meters does Andrew beat Carol?
 68. You have 50 red marbles and 50 blue marbles, other wise identical. You have 2 identical jars. A marble will be selected at random, from a jar selected at random. How would you apportion the marbles so as to maximise the chances of a red marble being selected?
68. You have 50 red marbles and 50 blue marbles, other wise identical. You have 2 identical jars. A marble will be selected at random, from a jar selected at random. How would you apportion the marbles so as to maximise the chances of a red marble being selected?
Can you prove it?
 66. A disease called The Phage spreading throughout a kingdom of 1,000,000 people. Currently one in every 500 people have the disease.
66. A disease called The Phage spreading throughout a kingdom of 1,000,000 people. Currently one in every 500 people have the disease.
The King's scientists develop a test with accuracy as follows: It will fail by false negative at a 1% rate. It will fail by false positive at a 2% rate. The King, planning to test everyone in the kingdom, is pleased. He thinks if he was prepared to secretly murder the 2,000 infected people a 2% rise wont make any difference. 'Hold on' says the chief nerd 'you'll actually have to murder X people and only one in Y of them will have The Phage.'
What are X & Y?
 64. 100 people stand in a circle in order 1 to 100. No. 1 has a sword. He kills the next person (i.e. No. 2) and gives the sword to the next living person (i.e. No. 3). All people do the same until only 1 survives. Which number survives to the end?
64. 100 people stand in a circle in order 1 to 100. No. 1 has a sword. He kills the next person (i.e. No. 2) and gives the sword to the next living person (i.e. No. 3). All people do the same until only 1 survives. Which number survives to the end?
 61. A bad king has a cellar of 1000 bottles of delightful and very expensive wine. A neighbouring queen plots to kill the bad king and sends a servant to poison the wine. Fortunately (or say unfortunately) the bad king's guards catch the servant after he has only poisoned one bottle. Alas, the guards don't know which bottle but know that the poison is so strong that even if diluted 100,000 times it would still kill the king. Furthermore, it takes around a month to have an effect. The bad king decides he will buy some slaves to drink the wine. Being a clever bad king he knows he need only buy 10 slaves and will still be able to drink the rest of the wine (999 bottles) at his anniversary party in 5 weeks time. Explain what is in the mind of the king, how will he be able to do so ?
61. A bad king has a cellar of 1000 bottles of delightful and very expensive wine. A neighbouring queen plots to kill the bad king and sends a servant to poison the wine. Fortunately (or say unfortunately) the bad king's guards catch the servant after he has only poisoned one bottle. Alas, the guards don't know which bottle but know that the poison is so strong that even if diluted 100,000 times it would still kill the king. Furthermore, it takes around a month to have an effect. The bad king decides he will buy some slaves to drink the wine. Being a clever bad king he knows he need only buy 10 slaves and will still be able to drink the rest of the wine (999 bottles) at his anniversary party in 5 weeks time. Explain what is in the mind of the king, how will he be able to do so ?
 60. There is a building of 100 floors
60. There is a building of 100 floors
-If an egg drops from the Nth floor or above it will break.
-If it's dropped from any floor below, it will not break.
You're given 2 eggs.
How do you find N in the minimum number of drops?
 57. How can you use a biased coin to make an unbiased decision?
57. How can you use a biased coin to make an unbiased decision?
That is to say the coin does not give heads or tales with equal probability. How can you ensure that decisions made with the coin do have a 50:50 chance?
 54. We are to play a version of Russian Roulette, the revolver is a standard six shooter but I will put two bullets in the gun in consecutive chambers. I spin the chambers, put the gun to my head pull the trigger and survive. I hand you the gun and give you a choice...
54. We are to play a version of Russian Roulette, the revolver is a standard six shooter but I will put two bullets in the gun in consecutive chambers. I spin the chambers, put the gun to my head pull the trigger and survive. I hand you the gun and give you a choice...
You may put the gun straight to your head and pull the trigger, or you may re-spin the gun before you do the same.
What is your choice and why? How does this differ from the case with only one bullet?
 52. Quickie: 100 black and white socks are in a drawer. How many socks must you pull out before you are guaranteed to have a pair?
52. Quickie: 100 black and white socks are in a drawer. How many socks must you pull out before you are guaranteed to have a pair?
Generalize to socks of N different colors.
(remember all the puzzles are logic, there's no slight of hand around here.)
 47. Watermelon is 99% water. I have 100 pounds of watermelon. After a week, drying in the sun, the shrivelled watermelon had only dried down to being 98% water. What is the total weight of the watermelon now?
47. Watermelon is 99% water. I have 100 pounds of watermelon. After a week, drying in the sun, the shrivelled watermelon had only dried down to being 98% water. What is the total weight of the watermelon now?
 46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?
46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?
How about other shapes, Square? N sides?
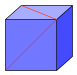 44. The two red lines in the diagram shown are drawn diagonally on the faces of a cube. What is the angle between them at the point where they join?
44. The two red lines in the diagram shown are drawn diagonally on the faces of a cube. What is the angle between them at the point where they join?
(click it to enlarge)
 39. An executioner lines up 100 prisoners single file and puts a red or a blue hat on each prisoner's head. Every prisoner can see the hats of the people in front of him in the line - but not his own hat, nor those of anyone behind him. The executioner starts at the end (back) and asks the last prisoner the colour of his hat. He must answer "red" or "blue." If he answers correctly, he is allowed to live. If he gives the wrong answer, he is killed instantly and silently. (While everyone hears the answer, no one knows whether an answer was right.) On the night before the line-up, the prisoners confer on strategy to help them. What should they do?
39. An executioner lines up 100 prisoners single file and puts a red or a blue hat on each prisoner's head. Every prisoner can see the hats of the people in front of him in the line - but not his own hat, nor those of anyone behind him. The executioner starts at the end (back) and asks the last prisoner the colour of his hat. He must answer "red" or "blue." If he answers correctly, he is allowed to live. If he gives the wrong answer, he is killed instantly and silently. (While everyone hears the answer, no one knows whether an answer was right.) On the night before the line-up, the prisoners confer on strategy to help them. What should they do?
 37. If an aeroplane makes a round trip and a wind is blowing, is the trip time shorter, longer or the same?
37. If an aeroplane makes a round trip and a wind is blowing, is the trip time shorter, longer or the same?
 35. A regular clock has an hour and minute hand. At 12 midnight the hands are exactly aligned. When is the next time they will exactly align or overlap? How many times a day will they overlap?
35. A regular clock has an hour and minute hand. At 12 midnight the hands are exactly aligned. When is the next time they will exactly align or overlap? How many times a day will they overlap?
 27. How many squares are there on a chessboard or checkerboard?? (the answer is not 64)
27. How many squares are there on a chessboard or checkerboard?? (the answer is not 64)
Can you extend your technique to calculate the number of rectangles on a chessboard?
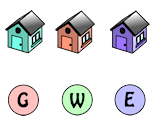 26. A man has built three houses. Nearby there are gas water and electric plants. The man wishes to connect all three houses to each of the gas, water and electricity supplies.
26. A man has built three houses. Nearby there are gas water and electric plants. The man wishes to connect all three houses to each of the gas, water and electricity supplies.
Unfortunately the pipes and cables must not cross each other. How would you connect each of the 3 houses to each of the gas, water and electricity supplies?
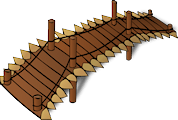 25. Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.
25. Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.
They only have one torch and it can't be thrown. Because of their different fitness levels and some minor injuries they can all cross at different speeds. Adam can cross in 1 minute, Bob in 2 minutes, Clair in 5 minutes and Dave in 10 minutes.
Adam, the brains of the group thinks for a moment and declares that the crossing can be completed in 17 minutes. There is no trick. How is this done?
 22. You have a 3 and a 5 litre water container, each container has no markings except for that which gives you it's total volume. You also have a running tap. You must use the containers and the tap in such away as to exactly measure out 4 litres of water. How is this done?
22. You have a 3 and a 5 litre water container, each container has no markings except for that which gives you it's total volume. You also have a running tap. You must use the containers and the tap in such away as to exactly measure out 4 litres of water. How is this done?
Can you generalise the form of your answer?
 20. How can this be true???? Have a look at the picture (click to enlarge.) All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from????
20. How can this be true???? Have a look at the picture (click to enlarge.) All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from????
 16. Quickie: You have a chessboard (8x8) plus a big box of dominoes (each 2x1). I use a marker pen to put an "X" in the squares at coordinates (1, 1) and (8, 8) - a pair of diagonally opposing corners. Is it possible to cover the remaining 62 squares using the dominoes without any of them sticking out over the edge of the board and without any of them overlapping? You cannot let the dominoes stand on their ends.
16. Quickie: You have a chessboard (8x8) plus a big box of dominoes (each 2x1). I use a marker pen to put an "X" in the squares at coordinates (1, 1) and (8, 8) - a pair of diagonally opposing corners. Is it possible to cover the remaining 62 squares using the dominoes without any of them sticking out over the edge of the board and without any of them overlapping? You cannot let the dominoes stand on their ends.
 10. You and I are to play a competitive game. We shall take it in turns to call out integers. The first person to call out '50' wins. The rules are as follows:
10. You and I are to play a competitive game. We shall take it in turns to call out integers. The first person to call out '50' wins. The rules are as follows:
–The player who starts must call out an integer between 1 and 10, inclusive;
–A new number called out must exceed the most recent number called by at least one and by no more than 10.
Do you want to go first, and if so, what is your strategy?
 6. There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.
6. There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.
Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6...). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9...). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
 5. How many degrees (if any) are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?
5. How many degrees (if any) are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?
 3. You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
3. You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
 This puzzle, along with #2 are incredibly difficult, I wish I'd never included them.
This puzzle, along with #2 are incredibly difficult, I wish I'd never included them.
1. You are given a set of scales and 12 marbles. The scales are of the old balance variety. That is, a small dish hangs from each end of a rod that is balanced in the middle. The device enables you to conclude either that the contents of the dishes weigh the same or that the dish that falls lower has heavier contents than the other.
The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of a different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more.
Note that the unusual marble may be heavier or lighter than the others. You are asked to both identify it and determine whether it is heavy or light.
Minimum Difficulty
Maximum Difficulty
88. Adam can mow a field in 1 hour, in the same time Bob can mow 2 fields, if they work together how long does it take them to mow a field?
And a generalised discussion of work-rate problems.
And a generalised discussion of work-rate problems.
 87. Quickie: Examine the diagram carefully. It shows a quadrant of a circle radius 'r', with a rectangle touching the perimeter of the circle. What is the length of the line labeled A-C.
87. Quickie: Examine the diagram carefully. It shows a quadrant of a circle radius 'r', with a rectangle touching the perimeter of the circle. What is the length of the line labeled A-C.(click image to enlarge)
86. Frosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.
For building material, Frosty has a spherical snowball with a 6 inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer. Can Frosty accomplish this?
For building material, Frosty has a spherical snowball with a 6 inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer. Can Frosty accomplish this?
 85. A man has a rectangular garden, 55m ('B' in the diagram,) by 40m('A',) and he makes a diagonal path, 1m wide, exactly in the manner indicated in the diagram. What is the area of the path?
85. A man has a rectangular garden, 55m ('B' in the diagram,) by 40m('A',) and he makes a diagonal path, 1m wide, exactly in the manner indicated in the diagram. What is the area of the path?(click image to enlarge)
 84. Two identical bolts are placed together so that their helical grooves intermesh. If you move the bolts around each other as you would twiddle your thumbs, holding each bolt firmly by the head so that it does not rotate and twiddling them in the direction shown, ill the heads a) move inward, b) move outward, or c) stay the same distance a from each other?
84. Two identical bolts are placed together so that their helical grooves intermesh. If you move the bolts around each other as you would twiddle your thumbs, holding each bolt firmly by the head so that it does not rotate and twiddling them in the direction shown, ill the heads a) move inward, b) move outward, or c) stay the same distance a from each other?(click image to enlarge)
83. Quickie: John runs a tennis club. He's to organise a knockout tournament. He puts out the sign up sheet and after a week he has 15 sign-ups. John is confused, he can't work out how to organise a knock out tournament with 15 players, and doesn't know how many courts to book.
He asks Arabella, the professor. She knows instantly, without giving it a second's thought...
How does Arabella do this? She doesn't have time to plan the whole tournament.
He asks Arabella, the professor. She knows instantly, without giving it a second's thought...
How does Arabella do this? She doesn't have time to plan the whole tournament.
 82. Quickie: A carpenter, working with a buzz saw, wishes to cut a wooden cube, three inches on each side, into 27 one-inch cubes. He can do it easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut?
82. Quickie: A carpenter, working with a buzz saw, wishes to cut a wooden cube, three inches on each side, into 27 one-inch cubes. He can do it easily by making six cuts through the cube, keeping the pieces together in the cube shape. Can he reduce the number of necessary cuts by rearranging the pieces after each cut?(click image to enlarge)
 81. The diagram shows the tracks from a two wheeled bicycle. Was the bicycle traveling from left to right or right to left?
81. The diagram shows the tracks from a two wheeled bicycle. Was the bicycle traveling from left to right or right to left?(click image to enlarge)
80. Quickie: Suppose I give you four cards labeled with the letters A and D and the numerals 3 and 6. It is known every card has a letter on one side and a number on the other. The rule of the game is that a card with a vowel on it always has an even number on the other side.
Which of the cards would you have to turn over to prove this rule to be true?
Which of the cards would you have to turn over to prove this rule to be true?
79. -Flatland is a plane extending infinitely in all directions. It has an infinite number of airfields no two of which are exactly the same distance apart.
-At a point in time a plane will take off from each airport and land at it's nearest neighbouring airport.
-What is the maximum number of aeroplanes that may land at any single airfield?
-At a point in time a plane will take off from each airport and land at it's nearest neighbouring airport.
-What is the maximum number of aeroplanes that may land at any single airfield?
 78. Secret Santa is a Western Christmas tradition in which members of a group or community are randomly assigned a person to whom they anonymously give a gift.
78. Secret Santa is a Western Christmas tradition in which members of a group or community are randomly assigned a person to whom they anonymously give a gift.The rules for determining who buys for whom are as follows. All the participants put their names in a hat. Each player will draw a name in turn. If they should draw their own name they will return it to the hat and draw another. If the last person to draw draws their own name the game is void and everyone starts again. Otherwise people will not return the name to the hat and will buy a present for the person whose name they have drawn.
Adam, Bob and Carol are to play a game of Secret Santa. They will draw in alphabetical order. What are the odds that Adam buys for Carol?
77. Quickie: A mother is 21 years older than her child. In exactly 6 years from now, the mother will be exactly 5 times as old as the child.
Where is the father?
Where is the father?
 76. The diagram shows two concentric annuli (two dimensional ring shapes,) given that the two red lines are the same length, prove that the shaded areas are the same too.
76. The diagram shows two concentric annuli (two dimensional ring shapes,) given that the two red lines are the same length, prove that the shaded areas are the same too.(click image to enlarge)
75. Three athletes (and only three athletes) participate in a series of track and field events. Points are awarded for 1st, 2nd, and 3rd place in each event (the same points for each event, i.e. 1st always gets "x" points, 2nd always gets "y" points, 3rd always gets "z" points), with x > y > z > 0, and all point values being integers.
The athletes are named Adam, Bob, and Charlie:
- Adam finished first overall with 22 points
- Bob won the Javelin event and finished with 9 points overall.
- Charlie also finished with 9 points overall.
Who finished second in the 100-meter dash (and why)?
The athletes are named Adam, Bob, and Charlie:
- Adam finished first overall with 22 points
- Bob won the Javelin event and finished with 9 points overall.
- Charlie also finished with 9 points overall.
Who finished second in the 100-meter dash (and why)?
 74. There are 100 prisoners in solitary cells. There's a central living room with one light bulb; this bulb is initially off. No prisoner can see the light bulb from his or her own cell. Everyday, the warden picks a prisoner equally at random, and that prisoner visits the living room. While there, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting that all 100 prisoners have been to the living room by now. If this assertion is false, all 100 prisoners are shot. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world could always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. The prisoners are allowed to get together one night in the courtyard, to discuss a plan. What plan should they agree on, so that eventually, someone will make a correct assertion?
74. There are 100 prisoners in solitary cells. There's a central living room with one light bulb; this bulb is initially off. No prisoner can see the light bulb from his or her own cell. Everyday, the warden picks a prisoner equally at random, and that prisoner visits the living room. While there, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting that all 100 prisoners have been to the living room by now. If this assertion is false, all 100 prisoners are shot. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world could always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. The prisoners are allowed to get together one night in the courtyard, to discuss a plan. What plan should they agree on, so that eventually, someone will make a correct assertion?
73. Quickie: What is the square root of 12345678987654321?
It's worth taking a clue on this one.
It's worth taking a clue on this one.
 72. A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4cm and it's length is 12cm.
72. A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4cm and it's length is 12cm.Find the length of the string.
71. You start in the top left corner of a 6x6 grid, your goal is to get to the bottom right corner. You can only move to the right or down. You can't move diagonally and you can't move backwards.
How many different ways are there to get from the start to the finish?
How many different ways are there to get from the start to the finish?
 70. Andrew, Britney and Carol race each other in a 100 meters race. All of them run at a constant speed throughout the race.
70. Andrew, Britney and Carol race each other in a 100 meters race. All of them run at a constant speed throughout the race.Andrew beats Britney by 20 meters.
Britney beats Carol by 20 meters.
By how many meters does Andrew beat Carol?
69. Quickie: At a whisky tasting Mr Cheap works out that for every 10 used, empty, glasses he can collect, he can poor the dregs together to make a whole new glass of whisky. At the end of the day he is able to find 100 empty glasses. How many full glasses can he now drink?
 68. You have 50 red marbles and 50 blue marbles, other wise identical. You have 2 identical jars. A marble will be selected at random, from a jar selected at random. How would you apportion the marbles so as to maximise the chances of a red marble being selected?
68. You have 50 red marbles and 50 blue marbles, other wise identical. You have 2 identical jars. A marble will be selected at random, from a jar selected at random. How would you apportion the marbles so as to maximise the chances of a red marble being selected?Can you prove it?
67. How far is the Horizon?
 66. A disease called The Phage spreading throughout a kingdom of 1,000,000 people. Currently one in every 500 people have the disease.
66. A disease called The Phage spreading throughout a kingdom of 1,000,000 people. Currently one in every 500 people have the disease.The King's scientists develop a test with accuracy as follows: It will fail by false negative at a 1% rate. It will fail by false positive at a 2% rate. The King, planning to test everyone in the kingdom, is pleased. He thinks if he was prepared to secretly murder the 2,000 infected people a 2% rise wont make any difference. 'Hold on' says the chief nerd 'you'll actually have to murder X people and only one in Y of them will have The Phage.'
What are X & Y?
65. Quickie: There are 9 coins, all except one are the same weight, the odd one is heavier than the rest. You must determine which is the odd one out using an old fashioned balance. You may use the balance twice. Explain how this can be done.
 64. 100 people stand in a circle in order 1 to 100. No. 1 has a sword. He kills the next person (i.e. No. 2) and gives the sword to the next living person (i.e. No. 3). All people do the same until only 1 survives. Which number survives to the end?
64. 100 people stand in a circle in order 1 to 100. No. 1 has a sword. He kills the next person (i.e. No. 2) and gives the sword to the next living person (i.e. No. 3). All people do the same until only 1 survives. Which number survives to the end?
63. Quickie: Billy The Whizz, a 19th century cowboy, carries an 1847 Colt single action 6 shooter revolver. So proficient is he with this weapon that when he fires all 6 shots in a row, the time between the first bullet and the last is 60 seconds. How long would it take him to fire 3 shots?
62. Quickie: A snail is at the bottom of a 30 foot well. Every hour the snail is able to climb up 3 feet, then immediately slide back down 2 feet. How many hours does it take for the snail to get out of the well?
 61. A bad king has a cellar of 1000 bottles of delightful and very expensive wine. A neighbouring queen plots to kill the bad king and sends a servant to poison the wine. Fortunately (or say unfortunately) the bad king's guards catch the servant after he has only poisoned one bottle. Alas, the guards don't know which bottle but know that the poison is so strong that even if diluted 100,000 times it would still kill the king. Furthermore, it takes around a month to have an effect. The bad king decides he will buy some slaves to drink the wine. Being a clever bad king he knows he need only buy 10 slaves and will still be able to drink the rest of the wine (999 bottles) at his anniversary party in 5 weeks time. Explain what is in the mind of the king, how will he be able to do so ?
61. A bad king has a cellar of 1000 bottles of delightful and very expensive wine. A neighbouring queen plots to kill the bad king and sends a servant to poison the wine. Fortunately (or say unfortunately) the bad king's guards catch the servant after he has only poisoned one bottle. Alas, the guards don't know which bottle but know that the poison is so strong that even if diluted 100,000 times it would still kill the king. Furthermore, it takes around a month to have an effect. The bad king decides he will buy some slaves to drink the wine. Being a clever bad king he knows he need only buy 10 slaves and will still be able to drink the rest of the wine (999 bottles) at his anniversary party in 5 weeks time. Explain what is in the mind of the king, how will he be able to do so ?
 60. There is a building of 100 floors
60. There is a building of 100 floors-If an egg drops from the Nth floor or above it will break.
-If it's dropped from any floor below, it will not break.
You're given 2 eggs.
How do you find N in the minimum number of drops?
59. You have 25 horses, you want to pick the fastest 3 horses out of those 25. In each race, only 5 horses can run at the same time. What is the minimum number of races required to find the 3 fastest horses without using a stopwatch?
58. Quickie: A blind man is alone on a deserted island. He has two blue pills and two red pills. He must take exactly one red pill and one blue pill or he will die. How does he do it?
 57. How can you use a biased coin to make an unbiased decision?
57. How can you use a biased coin to make an unbiased decision?That is to say the coin does not give heads or tales with equal probability. How can you ensure that decisions made with the coin do have a 50:50 chance?
56. A farmer is on his way back from the market, with him he has a fox, a chicken and some grain. When he reaches a river crossing he must use a small boat only big enough for him and one other item. Unfortunately if the fox is left alone with the chicken it will eat it, as will the chicken eat the grain. Explain how the farmer can cross the river.
55. There is a long line of people waiting outside a theatre to buy tickets. The theatre owner comes out and announces that the first person to have a birthday same as someone standing anywhere before him in the line gets a free ticket. Where will you stand to maximize your chance?
 54. We are to play a version of Russian Roulette, the revolver is a standard six shooter but I will put two bullets in the gun in consecutive chambers. I spin the chambers, put the gun to my head pull the trigger and survive. I hand you the gun and give you a choice...
54. We are to play a version of Russian Roulette, the revolver is a standard six shooter but I will put two bullets in the gun in consecutive chambers. I spin the chambers, put the gun to my head pull the trigger and survive. I hand you the gun and give you a choice...You may put the gun straight to your head and pull the trigger, or you may re-spin the gun before you do the same.
What is your choice and why? How does this differ from the case with only one bullet?
53. A train enters a station at 50m/s where it starts to decelerate uniformly, coming to a complete stop at the end of the platform. The distance from the entrance to the station to the platform end is 500m. At the exact same moment as the train enters the station a Bee takes off from the buffers at the end of the platform and heads towards the train, when it reaches the front of the train it turns around and heads back to where it started. It continues to do this, start of the platform, front of the train, start of the platform back and forth until the train stops where up on it is crushed.
If the speed of the Bee is 40m/s how far does the Bee travel?
You can expand this question to determine, for example, the time of the first impact or, is there such a thing as (and if so what is it,) a minimum speed the Bee needs to travel at in order to be able to perform this feat?
If the speed of the Bee is 40m/s how far does the Bee travel?
You can expand this question to determine, for example, the time of the first impact or, is there such a thing as (and if so what is it,) a minimum speed the Bee needs to travel at in order to be able to perform this feat?
 52. Quickie: 100 black and white socks are in a drawer. How many socks must you pull out before you are guaranteed to have a pair?
52. Quickie: 100 black and white socks are in a drawer. How many socks must you pull out before you are guaranteed to have a pair? Generalize to socks of N different colors.
(remember all the puzzles are logic, there's no slight of hand around here.)
51. Alice, Bob, and Cheri, three smart people, arrange a three-way duel. Alice is a poor shot, hitting her target only 1/3 of the time on average. Bob is better, hitting his target 2/3 of the time. Cheri is a sure shot hitting 100% of the time. They take turns shooting, first Alice, then Bob, the Cheri, then back to Alice, and so on until one is left. What is Alice's best course of action? And her chances of survival?
50. A man is looking at a photograph of someone. His friend asks who it is.
The man replies, 'Brothers and sisters, I have none. But that man's father is my father's son'.
Who is in the photograph?
The man replies, 'Brothers and sisters, I have none. But that man's father is my father's son'.
Who is in the photograph?
49. You reach a fork in the road. A sign explains that in one direction is Heaven and the other is Hell. Each path is blocked by a Guard. The sign goes on to say that one of the guards will always lie and the other will always tell the truth, it does not say which guard is which. We assume that the guards do know which path leads to where.
You may ask one question of only one guard in order that you can determine, with certainty, the way to Heaven. What is that question?
You may ask one question of only one guard in order that you can determine, with certainty, the way to Heaven. What is that question?
48. Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates.
May 15, May 16, May 19, June 17, June 18, July 14, July 16, August 14, August 15, August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don't know when Cheryl's birthday is, but I know that Bernard does not know too.
Bernard: At first I don't know when Cheryl's birthday is, but I know now.
Albert: Then I also know when Cheryl's birthday is.
So when is Cheryl's birthday?
May 15, May 16, May 19, June 17, June 18, July 14, July 16, August 14, August 15, August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don't know when Cheryl's birthday is, but I know that Bernard does not know too.
Bernard: At first I don't know when Cheryl's birthday is, but I know now.
Albert: Then I also know when Cheryl's birthday is.
So when is Cheryl's birthday?
 47. Watermelon is 99% water. I have 100 pounds of watermelon. After a week, drying in the sun, the shrivelled watermelon had only dried down to being 98% water. What is the total weight of the watermelon now?
47. Watermelon is 99% water. I have 100 pounds of watermelon. After a week, drying in the sun, the shrivelled watermelon had only dried down to being 98% water. What is the total weight of the watermelon now?
 46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?
46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?How about other shapes, Square? N sides?
45. A lady has two children. One is a boy. What are the chances of the other child also being a boy?
How does this change if you are told the oldest child is a boy?
How does this change if you are told the oldest child is a boy?
 44. The two red lines in the diagram shown are drawn diagonally on the faces of a cube. What is the angle between them at the point where they join?
44. The two red lines in the diagram shown are drawn diagonally on the faces of a cube. What is the angle between them at the point where they join?
(click it to enlarge)
43. You have 10 stacks of 10 gold coins. All of the coins in one of these stacks are counterfeit, all the other coins are not. A real coin weighs 10 grammes. A counterfeit coin weighs 11 grammes. You have a modern scale that provides an accurate readout. What is the minimum number of weighings needed to determine which stack is fake?
How about if you had 11 stacks?
How about if you had 11 stacks?
42. You are at a point on the Earth. You travel South 100 miles, East 100 Miles and North 100 Miles. You arrive back where you started. Where are you? You are NOT at the North Pole.
41. Suppose you tie a rope tightly around the Earth's equator. You add an extra 3 feet to the length. All around the Earth the rope is raised up uniformly as high as is possible to make it tight again. How high is that?
40. Using only a 4 minute and 7 minute hourglass or egg timer how would you measure exactly 9 minutes?
 39. An executioner lines up 100 prisoners single file and puts a red or a blue hat on each prisoner's head. Every prisoner can see the hats of the people in front of him in the line - but not his own hat, nor those of anyone behind him. The executioner starts at the end (back) and asks the last prisoner the colour of his hat. He must answer "red" or "blue." If he answers correctly, he is allowed to live. If he gives the wrong answer, he is killed instantly and silently. (While everyone hears the answer, no one knows whether an answer was right.) On the night before the line-up, the prisoners confer on strategy to help them. What should they do?
39. An executioner lines up 100 prisoners single file and puts a red or a blue hat on each prisoner's head. Every prisoner can see the hats of the people in front of him in the line - but not his own hat, nor those of anyone behind him. The executioner starts at the end (back) and asks the last prisoner the colour of his hat. He must answer "red" or "blue." If he answers correctly, he is allowed to live. If he gives the wrong answer, he is killed instantly and silently. (While everyone hears the answer, no one knows whether an answer was right.) On the night before the line-up, the prisoners confer on strategy to help them. What should they do?
38. On a deserted road, the probability of observing a car during a thirty-minute period is 95%. What is the chance of observing a car in a ten-minute period?
 37. If an aeroplane makes a round trip and a wind is blowing, is the trip time shorter, longer or the same?
37. If an aeroplane makes a round trip and a wind is blowing, is the trip time shorter, longer or the same?
36. You are in a dark room with a deck of cards. N of the cards are face up and the rest are face down. You can't see the cards. How do you divide the deck in to two piles with equal numbers of face up cards in each?
 35. A regular clock has an hour and minute hand. At 12 midnight the hands are exactly aligned. When is the next time they will exactly align or overlap? How many times a day will they overlap?
35. A regular clock has an hour and minute hand. At 12 midnight the hands are exactly aligned. When is the next time they will exactly align or overlap? How many times a day will they overlap?
34. A man has three daughters. A second, intelligent man, asked him the ages of his daughters. The first man told him that the product of their ages (them all multiplied together,) was 36. After thinking the second man was unable to find the answer and asked for another clue. The first man replies the sum of their ages is equal to his house door number. Still the second man was unable to answer and asked for another clue. The first man told him that his youngest daughter had blue eyes, and suddenly second man gave the correct answer. Explain how?
33. Assuming I want to stay dry. Should I walk or run in the rain?
32. Two creepers, (climbing plants,) one jasmine and other rose, are both climbing up and round a cylindrical tree trunk. Jasmine twists clockwise and rose anticlockwise, both start at the same point on the ground. Before they reach the first branch of the tree the jasmine had made 5 complete twists and the rose 3 twists. Not counting the bottom and the top, how many times do they cross?
31. Consider a standard chess board. What is the diameter of the largest circle that can be drawn on the board whilst only drawing on the black squares.
30. A drinks machine offers three selections - Tea, Coffee or Random but the machine has been wired up wrongly so that each button does not give what it claims. If each drink costs 50p, how much minimum money do you have to put into the machine to work out which button gives which selection ?
29. There were two men having a meal. The first man brought 5 loaves of bread, and the second brought 3. A third man, Ali, came and joined them. They together ate the whole 8 loaves. As he left Ali gave the men 8 coins as a thank you. The first man said that he would take 5 of the coins and give his partner 3, but the second man refused and asked for the half of the sum (i.e. 4 coins) as an equal division. The first one refused.
They went to Ali and asked for the fair solution. Ali told the second man, "I think it is better for you to accept your partner's offer." But the man refused and asked for justice. So Ali said, "then I say that who offered 5 loaves takes 7 coins, and who offered 3 loaves takes 1 coin."
Can you explain why this was actually fair?
They went to Ali and asked for the fair solution. Ali told the second man, "I think it is better for you to accept your partner's offer." But the man refused and asked for justice. So Ali said, "then I say that who offered 5 loaves takes 7 coins, and who offered 3 loaves takes 1 coin."
Can you explain why this was actually fair?
28. 3 men go into a hotel. The man behind the desk says a room is $30 so each man pays $10 and goes to the room.
A while later the man behind the desk realized the room was only $25 so he sent the bellboy to the 3 guys' room with $5. On the way the bellboy couldn't figure out how to split $5 evenly between 3 men, so he gave each man a $1 and kept the other $2 for himself.
This meant that the 3 men each paid $9 for the room, which is a total of $27 add the $2 that the bellboy kept = $29. Where is the other dollar?
A while later the man behind the desk realized the room was only $25 so he sent the bellboy to the 3 guys' room with $5. On the way the bellboy couldn't figure out how to split $5 evenly between 3 men, so he gave each man a $1 and kept the other $2 for himself.
This meant that the 3 men each paid $9 for the room, which is a total of $27 add the $2 that the bellboy kept = $29. Where is the other dollar?
 27. How many squares are there on a chessboard or checkerboard?? (the answer is not 64)
27. How many squares are there on a chessboard or checkerboard?? (the answer is not 64)
Can you extend your technique to calculate the number of rectangles on a chessboard?
 26. A man has built three houses. Nearby there are gas water and electric plants. The man wishes to connect all three houses to each of the gas, water and electricity supplies.
26. A man has built three houses. Nearby there are gas water and electric plants. The man wishes to connect all three houses to each of the gas, water and electricity supplies.Unfortunately the pipes and cables must not cross each other. How would you connect each of the 3 houses to each of the gas, water and electricity supplies?
 25. Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.
25. Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.They only have one torch and it can't be thrown. Because of their different fitness levels and some minor injuries they can all cross at different speeds. Adam can cross in 1 minute, Bob in 2 minutes, Clair in 5 minutes and Dave in 10 minutes.
Adam, the brains of the group thinks for a moment and declares that the crossing can be completed in 17 minutes. There is no trick. How is this done?
24. You're a farmer. You're going to a market to buy some animals. On the market there are 3 types of animals for sale. You can buy:
Horses for £10 each, goats for £1 each and ducks, you get 8 of these per bunch and each bunch costs £1. The aim is to acquire 100 animals at the cost of £100, what is the combination of horses, goats and duck that allows you to do this? (you must buy at least one of each.)
Horses for £10 each, goats for £1 each and ducks, you get 8 of these per bunch and each bunch costs £1. The aim is to acquire 100 animals at the cost of £100, what is the combination of horses, goats and duck that allows you to do this? (you must buy at least one of each.)
23. I have three envelopes, into one of them I put a £20 note. I lay the envelopes out on a table in front of me and allow you to pick one envelope. You hold but do not open this envelope. I then take one of the envelopes from the table, demonstrate to you that it was empty, screw it up and throw it away. The question is would you rather stick with the envelope you have selected or exchange it for the one on the table. Why? What would be the expected value to you of the exchange?
 22. You have a 3 and a 5 litre water container, each container has no markings except for that which gives you it's total volume. You also have a running tap. You must use the containers and the tap in such away as to exactly measure out 4 litres of water. How is this done?
22. You have a 3 and a 5 litre water container, each container has no markings except for that which gives you it's total volume. You also have a running tap. You must use the containers and the tap in such away as to exactly measure out 4 litres of water. How is this done?Can you generalise the form of your answer?
21. A man is in a rowing boat floating on a lake, in the boat he has a brick. He throws the brick over the side of the boat so as it lands in the water. The brick sinks quickly. The question is, as a result of this does the water level in the lake go up or down?
 20. How can this be true???? Have a look at the picture (click to enlarge.) All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from????
20. How can this be true???? Have a look at the picture (click to enlarge.) All the lines are straight, the shapes that make up the top picture are the same as the ones in the bottom picture so where does the gap come from????
19. How many consecutive zeros are there at the end of 100! (100 factorial). How would your solution change if the problem were in base 5? How about in Binary???
18. Quickie: Can the mean of any two consecutive prime numbers ever be prime?
17. Quickie: You have a string-like fuse that burns in exactly one minute. The fuse is inhomogeneous, and it may burn slowly at first, then quickly, then slowly, and so on. You have a box of matches, and no watch. How do you measure exactly 30 seconds?
If you had 2 fuses could you measure 45 seconds?
If you had 2 fuses could you measure 45 seconds?
 16. Quickie: You have a chessboard (8x8) plus a big box of dominoes (each 2x1). I use a marker pen to put an "X" in the squares at coordinates (1, 1) and (8, 8) - a pair of diagonally opposing corners. Is it possible to cover the remaining 62 squares using the dominoes without any of them sticking out over the edge of the board and without any of them overlapping? You cannot let the dominoes stand on their ends.
16. Quickie: You have a chessboard (8x8) plus a big box of dominoes (each 2x1). I use a marker pen to put an "X" in the squares at coordinates (1, 1) and (8, 8) - a pair of diagonally opposing corners. Is it possible to cover the remaining 62 squares using the dominoes without any of them sticking out over the edge of the board and without any of them overlapping? You cannot let the dominoes stand on their ends.
15. Why is it that if 'p' is a prime number bigger than 3, then p2-1 is always divisible by 24 with no remainder?
14. You have 52 playing cards (26 red, 26 black). You draw cards one by one. A red card pays you a dollar. A black one fines you a dollar. You can stop any time you want. Cards are not returned to the deck after being drawn. What is the optimal stopping rule in terms of maximizing expected payoff?
Also, what is the expected payoff following this optimal rule?
Also, what is the expected payoff following this optimal rule?
13. You are standing at the centre of a circular field of radius R. The field has a low wire fence around it. Attached to the wire fence (and restricted to running around the perimeter) is a large, sharp-fanged, hungry dog. You can run at speed v, while the dog can run four times as fast. What is your running strategy to escape the field?
12. Inside of a dark closet are five hats: three blue and two red. Knowing this, three smart men go into the closet, and each selects a hat in the dark and places it unseen upon his head.
Once outside the closet, no man can see his own hat. The first man looks at the other two, thinks, and says, "I cannot tell what color my hat is." The second man hears this, looks at the other two, and says, "I cannot tell what color my hat is either." The third man is blind. The blind man says, "Well, I know what color my hat is." What color is his hat?
Once outside the closet, no man can see his own hat. The first man looks at the other two, thinks, and says, "I cannot tell what color my hat is." The second man hears this, looks at the other two, and says, "I cannot tell what color my hat is either." The third man is blind. The blind man says, "Well, I know what color my hat is." What color is his hat?
11. You are to open a safe without knowing the combination. Beginning with the dial set at zero, the dial must be turned counter-clockwise to the first combination number, (then clockwise back to zero), and clockwise to the second combination number, (then counter-clockwise back to zero), and counter-clockwise again to the third and final number, where upon the door shall immediately spring open. There are 40 numbers on the dial, including the zero.
Without knowing the combination numbers, what is the maximum number of trials required to open the safe (one trial equals one attempt to dial a full three-number combination)?
Without knowing the combination numbers, what is the maximum number of trials required to open the safe (one trial equals one attempt to dial a full three-number combination)?
 10. You and I are to play a competitive game. We shall take it in turns to call out integers. The first person to call out '50' wins. The rules are as follows:
10. You and I are to play a competitive game. We shall take it in turns to call out integers. The first person to call out '50' wins. The rules are as follows:–The player who starts must call out an integer between 1 and 10, inclusive;
–A new number called out must exceed the most recent number called by at least one and by no more than 10.
Do you want to go first, and if so, what is your strategy?
9. In a certain matriarchal town, the women all believe in an old prophecy that says there will come a time when a stranger will visit the town and announce whether any of the men folks are cheating on their wives. The stranger will simply say "yes" or "no", without announcing the number of men implicated or their identities. If the stranger arrives and makes his announcement, the women know that they must follow a particular rule: If on any day following the stranger's announcement a woman deduces that her husband is not faithful to her, she must kick him out into the street at 10 A.M. the next day. This action is immediately observable by every resident in the town. It is well known that each wife is already observant enough to know whether any man (except her own husband) is cheating on his wife. However, no woman can reveal that information to any other. A cheating husband is also assumed to remain silent about his infidelity.
The time comes, and a stranger arrives. He announces that there are cheating men in the town. On the morning of the 10th day following the stranger's arrival, some unfaithful men are kicked out into the street for the first time. How many of them are there?
The time comes, and a stranger arrives. He announces that there are cheating men in the town. On the morning of the 10th day following the stranger's arrival, some unfaithful men are kicked out into the street for the first time. How many of them are there?
8. What is the smallest positive integer that leaves a remainder of 1 when divided by 2, remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and so on up to a remainder of 9 when divided by 10?
7. A windowless room contains three identical light fixtures, each containing an identical light bulb or light globe. Each light is connected to one of three switches outside of the room. Each bulb is switched off at present. You are outside the room, and the door is closed. Before opening the door you may play around with the light switches as many times as you like. But once you've opened the door, you may no longer touch a switch. After this, you go into the room and examine the lights. How can you tell which switch goes to which light?
 6. There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.
6. There are 100 light bulbs lined up in a row in a long room. Each bulb has its own switch and is currently switched off. The room has an entry door and an exit door. There are 100 people lined up outside the entry door. Each bulb is numbered consecutively from 1 to 100. So is each person.Person No. 1 enters the room, switches on every bulb, and exits. Person No. 2 enters and flips the switch on every second bulb (turning off bulbs 2, 4, 6...). Person No. 3 enters and flips the switch on every third bulb (changing the state on bulbs 3, 6, 9...). This continues until all 100 people have passed through the room.
What is the final state of bulb No. 64? And how many of the light bulbs are illuminated after the 100th person has passed through the room?
 5. How many degrees (if any) are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?
5. How many degrees (if any) are there in the angle between the hour and minute hands of a clock when the time is a quarter past three?
4. A mythical city contains 100,000 married couples but no children. Each family wishes to "continue the male line", but they do not wish to over-populate. So, each family has one baby per annum until the arrival of the first boy. For example, if (at some future date) a family has five children, then it must be either that they are all girls, and another child is planned, or that there are four girls and one boy, and no more children are planned. Assume that children are equally likely to be born male or female.
Let p(t) be the percentage of children that are male at the end of year t. How is this percentage expected to evolve through time?
Let p(t) be the percentage of children that are male at the end of year t. How is this percentage expected to evolve through time?
 3. You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
3. You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
2. You are given a set of scales and 90 coins. The scales are of the same type as above. You must pay $100 every time you use the scales.
The 90 coins appear to be identical. In fact, 89 of them are identical, and one is of a different weight. Your task is to identify the unusual coin and to discard it while minimizing the maximum possible cost of weighing (another task might be to minimizing the expected cost of weighing). What is your algorithm to complete this task? What is the most it can cost to identify the unusual coin?
The 90 coins appear to be identical. In fact, 89 of them are identical, and one is of a different weight. Your task is to identify the unusual coin and to discard it while minimizing the maximum possible cost of weighing (another task might be to minimizing the expected cost of weighing). What is your algorithm to complete this task? What is the most it can cost to identify the unusual coin?
 This puzzle, along with #2 are incredibly difficult, I wish I'd never included them.
This puzzle, along with #2 are incredibly difficult, I wish I'd never included them.1. You are given a set of scales and 12 marbles. The scales are of the old balance variety. That is, a small dish hangs from each end of a rod that is balanced in the middle. The device enables you to conclude either that the contents of the dishes weigh the same or that the dish that falls lower has heavier contents than the other.
The 12 marbles appear to be identical. In fact, 11 of them are identical, and one is of a different weight. Your task is to identify the unusual marble and discard it. You are allowed to use the scales three times if you wish, but no more.
Note that the unusual marble may be heavier or lighter than the others. You are asked to both identify it and determine whether it is heavy or light.
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.






