Answer to Puzzle #36: N Face Up Cards In A Dark Room
36. You are in a dark room with a deck of cards. N of the cards are face up and the rest are face down. You can't see the cards. How do you divide the deck in to two piles with equal numbers of face up cards in each?
Unusually this puzzle was sent to me not through the site but by a real world friend:
Before reading the answer can I interest you in a clue?
First thing we need to clarify is what the puzzle doesn't say. It doesn't say we need to create two equal piles of 26 cards. It just says two piles with the same number of face up cards, nothing about the number of face down cards. It doesn't say that they need to be the same cards that are face up as at the start of the puzzle or that the same number of cards should be face up. It is assumed that we know the value of N.
The hard part here is not going to be me telling you the the answer, it's proving it to you.
The answer is: we take N cards, any N cards, from the deck to form a second pile and flip all the cards in the second pile. The second pile will then contain as many face up cards as the first pile.
This is difficult to get your head around so we'll look at some examples before we look at the maths. Consider the following deck. Blue is face down, red is face up and N=10, there are 10 face up cards..
We'll extract 10 or N from the deck. Remember it could be any 10, since we can't see the deck it doesn't matter if we took them from the middle, the end or randomly through out the deck. Pile 1 now has 42 cards, Pile 2 has 10
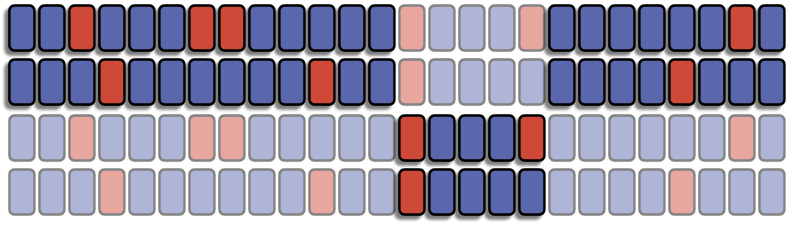
And now we turn over the cards we took.
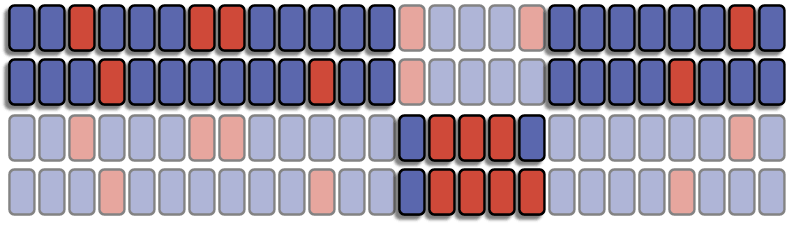
You can see in this case each pile contains 7 face up cards.
What if N=1, there is only one face up card. We'll we extract N or 1 card from the deck. In the most likely case we will have extracted a face down card we will then flip it to become face up, each pile will have 1 face up card. But if by chance we take the 1 face up card when we flip it in Pile 2 each pile will have no face up cards.
N>26 This was my next "ah but..." Let's say N is really big like 50. And when we split the deck of the 52 cards we take we pick up 49 face up cards and 1 face down, which leaves 1 face up in Pile 1. When we flip Pile 2 we will have 49 face down cards and 1 face up, the same as Pile 1.
Both AI's got this equally wrong. In the same way too.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
First thing we need to clarify is what the puzzle doesn't say. It doesn't say we need to create two equal piles of 26 cards. It just says two piles with the same number of face up cards, nothing about the number of face down cards. It doesn't say that they need to be the same cards that are face up as at the start of the puzzle or that the same number of cards should be face up. It is assumed that we know the value of N.
The hard part here is not going to be me telling you the the answer, it's proving it to you.
The answer is: we take N cards, any N cards, from the deck to form a second pile and flip all the cards in the second pile. The second pile will then contain as many face up cards as the first pile.
This is difficult to get your head around so we'll look at some examples before we look at the maths. Consider the following deck. Blue is face down, red is face up and N=10, there are 10 face up cards..
We'll extract 10 or N from the deck. Remember it could be any 10, since we can't see the deck it doesn't matter if we took them from the middle, the end or randomly through out the deck. Pile 1 now has 42 cards, Pile 2 has 10
And now we turn over the cards we took.
You can see in this case each pile contains 7 face up cards.
Ah But What About...
It's still hard to follow, so we'll consider some special cases.What if N=1, there is only one face up card. We'll we extract N or 1 card from the deck. In the most likely case we will have extracted a face down card we will then flip it to become face up, each pile will have 1 face up card. But if by chance we take the 1 face up card when we flip it in Pile 2 each pile will have no face up cards.
N>26 This was my next "ah but..." Let's say N is really big like 50. And when we split the deck of the 52 cards we take we pick up 49 face up cards and 1 face down, which leaves 1 face up in Pile 1. When we flip Pile 2 we will have 49 face down cards and 1 face up, the same as Pile 1.
The Generalised Case
There are N face up cards in Pile 1. We take N cards from Pile 1 to form Pile 2. Lets say, by chance F of those are face up. This necessarily leaves N-F face up cards in Pile 1. Pile 2 contains N cards, F of which are face up, meaning N-F are face down. When we flip over Pile 2 these N-F face down card become face up. Both piles contain N-F face up cards.Both AI's got this equally wrong. In the same way too.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
