Answer to Riddle #71: 6x6 Grid, How Many Ways?

71. You start in the top left corner of a 6x6 grid, your goal is to get to the bottom right corner. You can only move to the right or down. You can't move diagonally and you can't move backwards.

How many different ways are there to get from the start to the finish?

So we're saying all of the routes shown in the diagram would be acceptable. Interesting puzzle it relates to Pascal's Triangle which, in turn relates to just about everything:

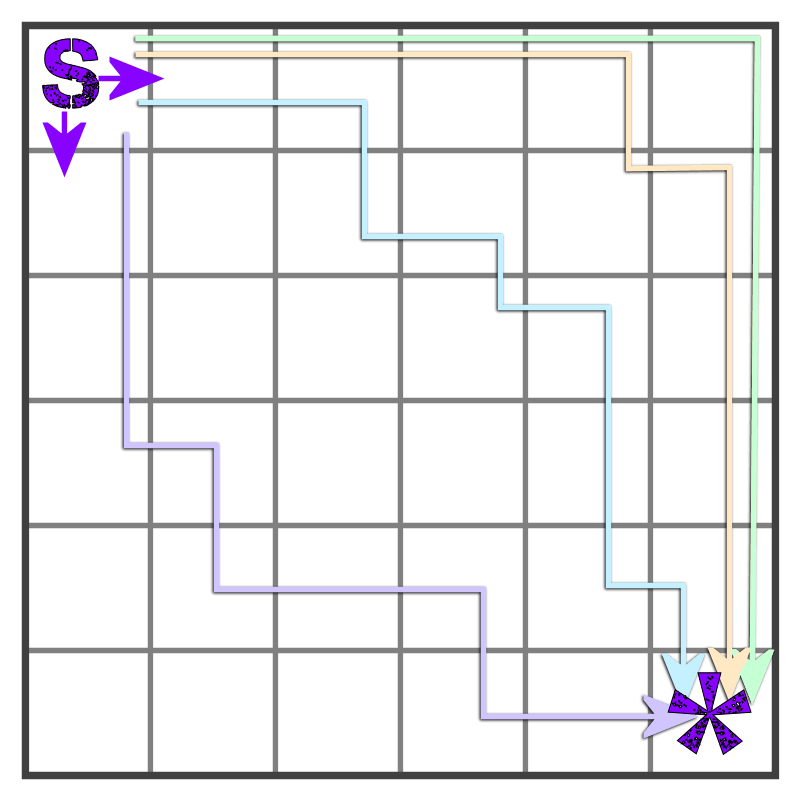6x6 grid showing acceptable roots to solve the puzzle

Before reading the answer can I interest you in a clue?

There's a key realisation here that a square can only be reached by the one above it or to the left of it. And therefore the number of possible ways of reaching it is the number of ways of reaching the square above it plus the number of ways of reaching the square to the left of it...
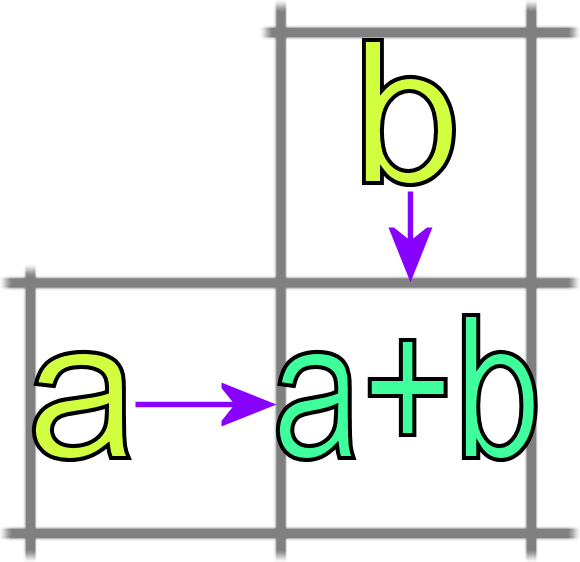
portion of 6x6 grid showing vertical and horizontal movement

portion of 6x6 grid showing vertical and horizontal movement

Take a moment to think about why, it can take a moment. Remember we are not counting the moves, but the possible combinations of different moves.

From here it's not that difficult to fill in the grid with the number of possible combinations of moves to reach each square. We know that there is only one way of reaching any square in the top row, similarly every square in the left hand column. Then just fill in the numbers...
full 6 by 6 grid showing the binomial numbers that represent the number of possible ways to get to that square.

full 6 by 6 grid showing the binomial numbers that represent the number of possible ways to get to that square.

Mathematics Nomenclature

We like to stay away from formal maths here relying on common sense. But it's possibly worth pointing out that 252 = ¹⁰C₅ Not surprising given we have 10 moves necessary 5 horizontal and 5 vertical in any combination.

Another result for Google

If you're curious what Bard made of this puzzle...

There are 252 different ways to get from the start to the finish.

To solve this problem, we can use the concept of binomial coefficients. A binomial coefficient is a number that counts the number of ways to choose k objects from a set of n objects, where order does not matter. The formula for a binomial coefficient is:

C(n, k) = n! / (k! * (n - k)!)

In this problem, we have n = 10 (the total number of moves) and k = 5 (the number of moves down). So, the number of ways to get from the start to the finish is:

C(10, 5) = 10! / (5! * 5!) = 252

If you're curious what ChatGPT made of this puzzle...

Where next?
List of Puzzles Random Puzzle Next Puzzle

© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.

PayPal - The safer, easier way to pay online.

PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel

Answer to Riddle #71: 6x6 Grid, How Many Ways?

Mathematics Nomenclature

This Website Uses Cookies