Answer to Puzzle #46: Three Ants on The Corners of a Triangle
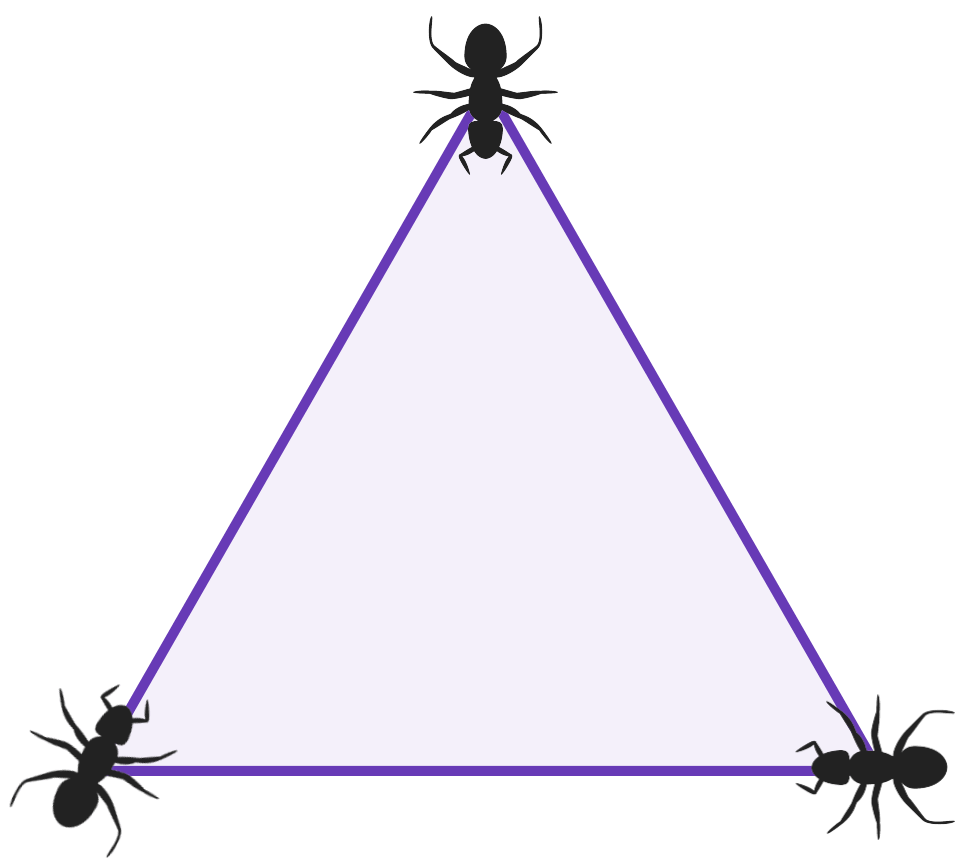
 46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?
46. Three ants are sitting at the three corners of an equilateral triangle. Each ant randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?How about other shapes, Square? N sides?
This problem looks quite hard but turns out to be fairly easy. Which for me at least is preferable to looks easy is hard:
 Before reading the answer can I interest you in a clue?
Before reading the answer can I interest you in a clue?In order that there is no collision we require that all the ants move in the same direction. Either all clockwise or all anticlockwise.
We assume the ants have a 50/50 chance of picking either direction. So the probability of them all deciding to go clockwise is given by ½•½•½ = 0.125
The probability of them all deciding to go anticlockwise equally is given by ½•½•½ = 0.125
Either of these will do so we can add the probabilities to make 0.25
There is another approach that perhaps requires slightly less understanding of probability. With three things each having two choices we have 2x2x2 = 8 possible configurations. If 'A' indicates anticlockwise and 'C' clockwise they are AAA, AAC, ACA, ACC, CAA, CAC, CCA & CCC. Of these 8 only 2 are of use to us. AAA and CCC. 2 of 8 is ¼ or 0.25
Square, N sided Polygon
Using the first approach for the triangle we had 2•½•½•½ or 2•(½^n) or 1/2n-1 or 2-(n-1) where n was equal to 3. We can see trivially that for a square the answer will be 1/8Using the other approach we have that there are 2n configurations, of which 2 will be useful to us. 2/2n brings us to 1/2n-1
Another extension
The next obvious extension is to consider four ants on a tetrahedron or triangular based pyramid.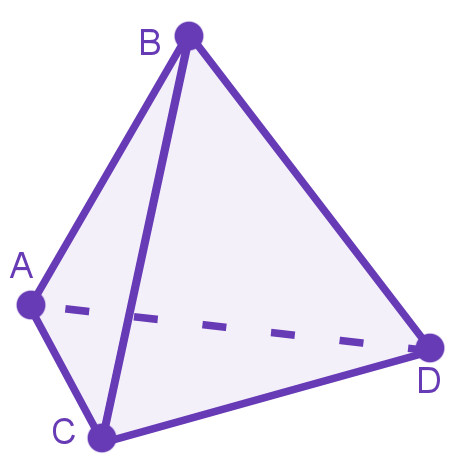
For a triangular based pyramid an ant at any of the 4 vertices can travel to each and every other vertex. If you labelled each vertex A, B, C & D then the ant starting at A can move to B, C & D, the ant starting at B can move to A, C & D and so on. There are 4 ants and each has 3 possible destinations meaning there are 34 = 81 possible outcomes. The question is how many of these don't involve a collision...
So let's consider the points as labelled A,B,C,D and lets call the ants starting at those positions a,b,c,d. To work towards the number of collision free outcomes we could just write down all the possible permutations of a,b,c,d and examine them there are only 24....
Instead I used a spread sheet to show all the outcomes in which each ant moves and count how many of the outcomes involved a unique ant on each vertex. (I believe these are called derangements.) You can view here. It shows 9 of the 81 are unique. They are badc bcda bdac cadb cdab cdba dabc dcab & dcba. But that sadly is not the full story.
Consider badc: There is a unique ant on each vertex, but the ant from A and the ant from B have swapped, so they would have run in to each other on the way. Similarly with cdab and dcba involve swaps c & a and d & a respectively. Which leaves us with 6 viable solutions out of the 81 moves we started with. I feel sure there is a nicer way of explaining this. 2 /27
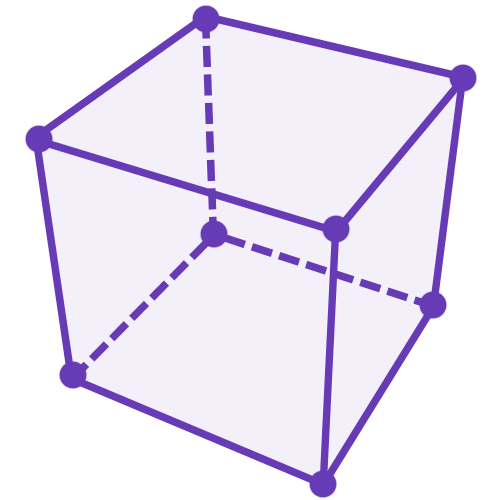
The cube is even more complicated, 8 ants or vertices each with 3 possible destinations gives 6,561. There certainly are viable outcomes, for example you could imagine the cube as two facing squares each end independent of each other. I'm not sure of the best way to work this out, but I will...
Assumptions
I think it's fairly clear that there are no real ants, the ants are just a device for explaining the puzzle. Nonetheless assumptions might be that the ants direction picking is unbiased, and that they move with the same speed.Both AI's got this.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.



