Answer to Puzzle #55: Free Theatre Tickets for the First Person With a Birthday the Same as Someone in Front of Them in the Queue
55. There is a long line of people waiting outside a theatre to buy tickets. The theatre owner comes out and announces that the first person to have a birthday same as someone standing anywhere before him in the line gets a free ticket. Where will you stand to maximize your chance?
I found this at the same time as the previous puzzle, it's a lot more complicated but I have seen it explained in a way that makes it seem more complicated than it need be, the same answer copied and paste all over the place, with seemingly no understanding. Let's see if we can do it in a way that is a bit more intuitive. We'll start by looking at something called the Birthday Paradox:
Before reading the answer can I interest you in a clue?The Birthday Paradox or problem asks how large a group of people one would need in order that it becomes likely that 2 of them have their birthday on the same day (of the year.) It's a nice problem and I have thought about including it itself. Intuitively people seem to guess about 180, but that is the answer to a different question... That is answering the probability that one specific person has the same birthday as anyone else. It misses out the cross combinations. A bit like the handshake puzzle.
The actual answer turns out to be, surprisingly I suppose, 23. The solution to the Birthday paradox is well known, nonetheless we shall derive it. The form will be that of a probability function that happens to go over 0.5 for first time at a value of n = 23. We will reason the following... The difference between P(n) and P(n-1) is the amount person n added to the cumulative probability and therefore the probability that he will be involved in the Birthday pairing.
The Birthday Paradox
We will be working with the probability that people do not have the same birthday. Why? The first person can't have the same birthday as anyone less by themselves, so lets look at the second person. At the point where we add the second person there is a 364/365 chance of them not sharing a birthday with the previous person. When we add the 3rd person there is there is a 363/365 chance of them not sharing a birthday and so on such that the nth person when added has a probability of not forming a share of (365 -n +1)/365. We can multiply these together to p(n') where that is the probability of, after n people we do not have a pair. n! is n factorial.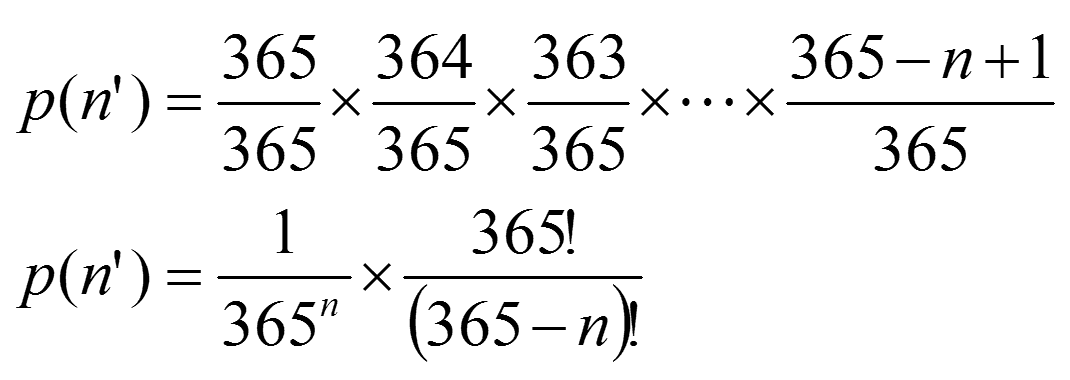
It's probably worth some exposition as to how we make the step... 100 x 99 x 98 x 97 x 96 x 95 x 94 x 93 x 92 x 91 = 100!/90!Which is a perfectly good equation for p(n') or 1 - p(n) save one thing. 365! is roughly equal to 2.51x10778 and so it's difficult to calculate so we must re arrange a little p(n') = 365Pn/365n where P indicates the Permutation function. The permutation function is defined exactly as we are using it, 365Pn is defined as 365!/(365-n)!. We're using this simply because we can calculate it, there is a button on a calculator and a function PERMUT(365,n) we can use in spreadsheet.
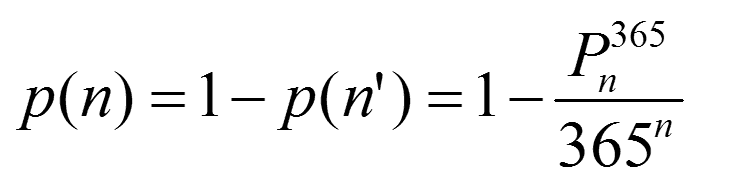If you punch in the number 23 you get a value of 0.507297234, this is the first time p(n) is greater than 0.5 and hence the reason why the answer to the birthday paradox is 23. The distribution is shown in the graph below.Back to the Theatre
We postulated above that the difference between p(n) and p(n-1) would be the probability added by person n. As such we should maximise this. Overlaid on the graph is the change in p(n) for each person. (Scale on the right.)As can be seen from the graph or read from the data that person 20 has the greatest contribution to the probability function, and therefore the greatest chance of being the one who adds a birthday pair.
You maximise your chances of winning the tickets by standing in position 20.
Assumptions
We assume that birthdays are independent and randomly distributed throughout the year, something we know not to be true. Birthrates vary throughout the year, there may be twins. We've completely ignored leap years. These are all reasonable assumptions but could you defend them?Neither of the AI's did very well with this one. To be fair it is a very complicated puzzle. See the discussion in the answer that ChatGPT gave.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
