Answer to Riddle #76: Area of an Annulus

Before reading the answer can I interest you in a clue?

Let's just crack in to the geometry. Essentially and obviously the area of an annulus (ring) is calculated by working out the area of the outer circle and subtracting from it the area of the inner circle.

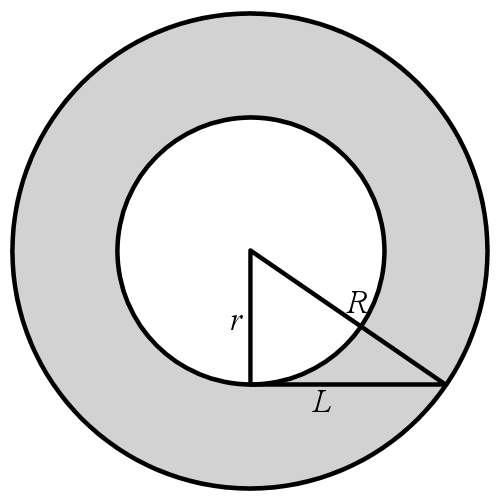
So the area of our annulus is the area of the big circle minus the area of the little

Area = πR² - πr²
Area = π(R²-r²)

We're going to need to need to show that we can eliminate r and R and thus prove the area is only dependent on L. Lets take a look with Pythagoras and see what happens. rRL is a right angle triangle where R is the hypotenuse. Pythagoras gives:

R² = r² + L²
L² = R² - r²

We can substitute R² - r² back in to the equation for area we had above:

Area = πL²

Which is sufficient to prove that if the red line is the same length then in the question then the area is the same.

Let's phrase it like a puzzle

A mad professor lives at the top of a light house. He wants the ground floor covered with carpet tiles. He calls a flooring company and explains that the room is ring shaped. The company explains that their carpet tiles are 1m² and they will need to send someone out to measure to see how many tiles they need to buy.

The worker visits the lighthouse to measure the sizes but finds the door locked and the following note pinned to the door.

Satisfied the worker goes back to the flooring shop and gets a clip around the ear. His boss said he was an idiot and they needed to know the exact measurements to work out the area. 'I know the area' said the worker.

What is it?

the area is πL² = π•50² = 7854m²