Answer to Riddle #72: Length of Rope Around a Rod?
72. A string is wound symmetrically around a circular rod. The string goes exactly 4 times around the rod. The circumference of the rod is 4cm and it's length is 12cm.
Find the length of the string.
Find the length of the string.
This is not actually that difficult. It involves no more than high school geometry. So if you're struggling you probably haven't figured out the right approach:
Before reading the answer can I interest you in a clue?Apparently an enormous number of people get this wrong. It took me a while too. People consider polar coordinates, all sorts of things. It's simply not necessary.
We are going to cut the tube, or imagine cutting the tube, at the point where the rope first appears and lay it flat. Once you see what this looks like I'm sure the solution will become trivial.
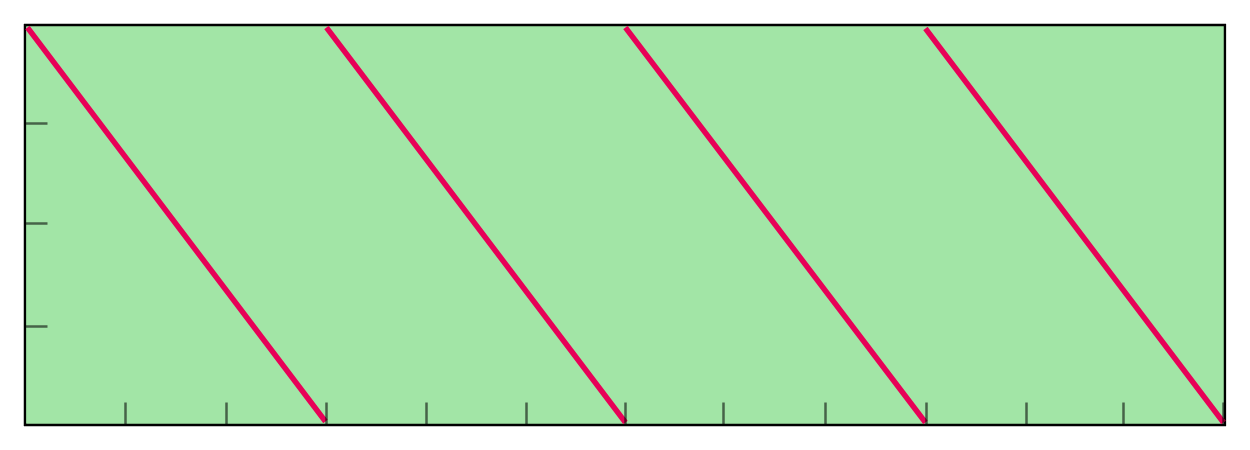
From here it's just a bit of Pythagoras Theorem. Notably this is a 3,4,5 Triangle (32 + 42 = 52.) So the hypotenuse is 5cm. We're interested in the total length of the diagonals, of which there are 4. So the rope is 20cm long.
Assumptions
We're assuming that the rope is, what is usually referred to in physics as, 'infinitely thin.' Which is usually taken to mean it can be discounted.Bard didn't even break a sweat with this one, ChatGPT however... If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
