Answer to Puzzle #41: Rope Around the Earth
41. Suppose you tie a rope tightly around the Earth's equator. You add an extra 3 feet to the length. All around the Earth the rope is raised up uniformly as high as is possible to make it tight again. How high is that?
This puzzle is old, a version of it appears in William Whiston's The Elements of Euclid circa 1702. More latterly it appears in Showtime drama 'House of Lies' about a group of management consultants.
Before reading the answer can I interest you in a clue?This puzzle is not so much hard as the result is surprising. Even as a I write it I know the answer is correct but it still doesn't sit well. Because of this we are going to do a rigorous mathematical treatment.
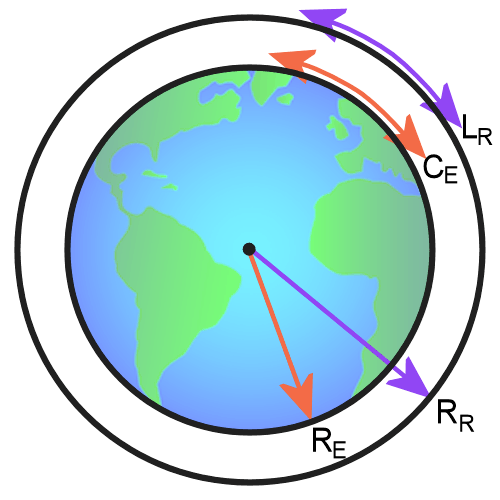
Let CE be the circumference of the Earth, LR be the new length of the rope, RE & RR be the radius from the center of the Earth to the edge and the new rope respectively. We are interested in what we will call H = RR - RE. Let's call X the amount we add to the length of the rope, in our case 3 feet. Additionally we know the relationship between the circumference of a circle and it's radius is generally given by R = C/2π that is the only formula you need to know to solve this puzzle. Plus some basic algebra.
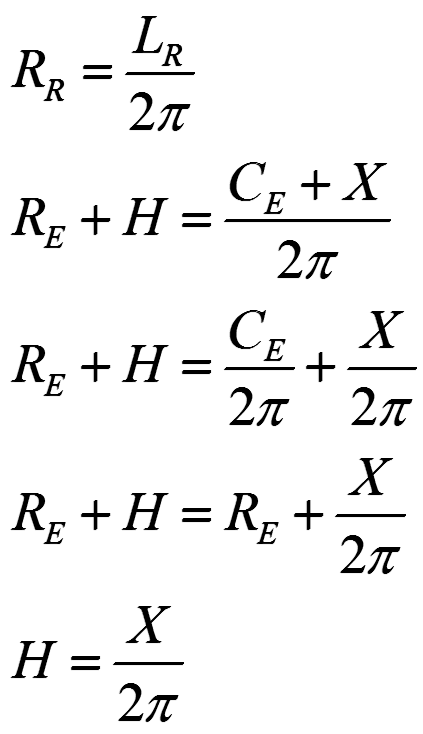
So for us the answer is 5.73 inches. (X is 36 inches.) In an interview a bit less than 6 would be sufficient. Basically it's 3 feet or 36 inches, over 2π.
What Happened?
The key thing to note is that the radius or circumference of the Earth do not feature in the result at all. They dropped out of the equations. In fact the answer would be the same if you tied a rope around your waist and added 3 feet to that. Tough to accept I know. But it's true.Still Can't Visualise it?
Ben Arnold came up with this explanation, said it helped him. The problem is that the length added to the rope seems so trivial compared radius of the earth it just seems implausible that it would raise the rope by so much. Consider the following diagram:
The idea is to imagine the earth is a cube or just a square really and ask yourself if you added, say 8 feet, to the rope, how far would that raise it above the square earth? From the diagram it's pretty clear it's one foot.
From there it's not hard to believe that adding 3 feet to a rope around the actual earth would raise it almost 6 inches.
Another one where the AI's really struggled. I can't imagine why either, it's a fairly standard puzzle.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
