Answer to Puzzle #33: Should I Walk or Run in the Rain

Before reading the answer can I interest you in a clue?

We are assuming that you have a specific distance you need to cover, for example you want to get from your house to your car. The confusion with this puzzle seems to stem from the notion that by walking quickly you are in the rain for less time, but that you invite some of the falling rain to hit you on the front as you travel through it. Where as if you move slowly you are in the rain for longer, but you only get the rain landing on your head.

In science as in these puzzles a useful technique is to look at your model 'in the limit.' That is to say, consider what would happen if you pushed one of your variables to the extreme edge, and see if this tells you anything you can use in the range you are interested in. Since we are interested in speed we will look at two extreme examples.

Extreme Slow, Stationary:

Well this is not rocket science, if you walk very very slowly you will be in the rain for a very long time and will get very wet. What's more it is clear, intuitively that if you speed up just slightly you will reduce your time in the rain and get less wet. At extreme slow speeds thinking about the rain hitting your front is clearly not necessary, if you are moving so slowly that a slight increase in speed causes your journey from your house to your car to take one hour instead of two you will obviously get wet less in one hour.

Some people will point out that if you are stationary in the rain you will get less wet in say one minute, than someone walking in the rain. Whilst this is obviously true it is irrelevant, you are trading slightly less wet for an infinite amount of time.

Extreme Fast, Speed of Light:

When travelling at the speed of light, or indeed just very very fast relative to the speed of the rain, we will scoop out a path in the rain. A horizontal column in the shape of our silhouette, (as shown,) all the rain in that volume will hit us on the front, instantly as if the rain were frozen in time. But importantly no rain will hit us on the head because we are exposed for zero time. What's more we can consider what might happen if we slowed down a bit... We will still scoop out the column of rain, but additionally we will get some rain on our heads. Infact we can not avoid scooping out the column of rain, not matter how slowly we move we will always scoop out this same volume. (see note.) Only the amount that falls on our heads is adjustable, and this is determined by the speed. Graphing the Wetness against Speed would show the wetness approaching the speed-of-light-wetness W_min as speed increases.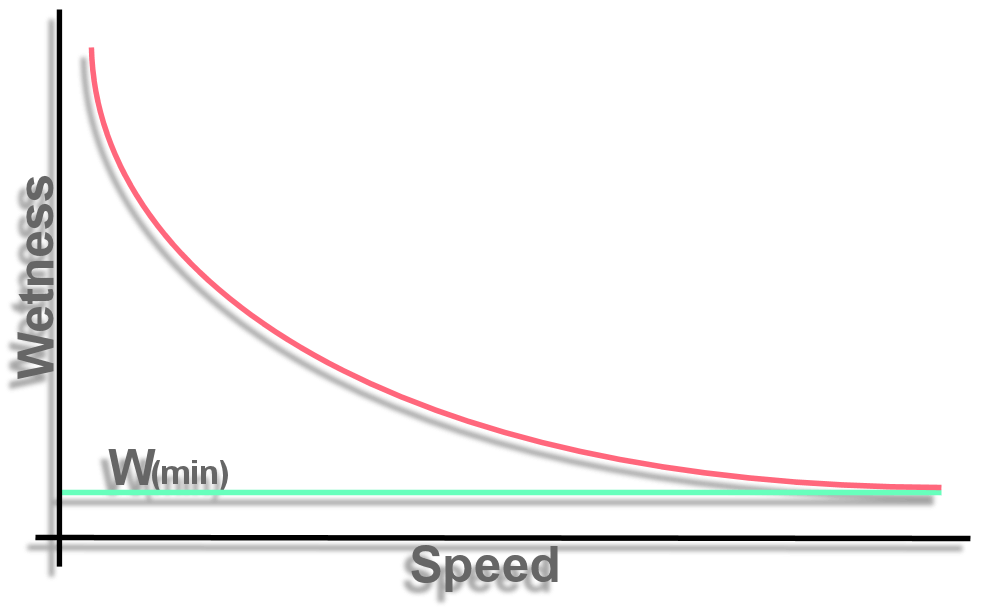


Finally, obviously we haven't considered the direction of the rain. But on average rain falls down, and when you are running you need to get where you are going. The conclusion is that moving as fast as you can will get you the least wet. Don't slip.

Why we always scoop the same rain:

Since first publishing this answer I have been asked to explain why we will always scoop out the same volume and pick up the same number of raindrops on our front. I can see that it might not be intuitive and it is fundamental to understanding the conclusion. To a physicist I would say on a macroscopic level we can consider point raindrops in a probability density function. Intuitively it seems unlikely that slowly walking forward we will walk into a fast-falling raindrops. I suppose it is unlikely, but if we are moving slowly we will have plenty of time. And these two effects cancel each other out. There are two approaches that I think might help. 1) Think of driving a flat fronted bus in straight falling ran. No matter how slowly you drive you will get some rain on your windscreen. The total result on the front of the bus is as if the bus were stationary and the rain were coming toward it with the speed the bus had. No matter how slight this is the front of the bus will pick up some rain. 2) The probability density function argument. In the tunnel we scoop out that I have mentioned before, rain is entering that tunnel from the top at the same rate it is leaving it from the bottom. There is always the same amount of rain in the tunnel. If we are moving through that tunnel we are necessarily encountering all that rain. It's no different from if the rain were stationary and held in a sort of fog.



They basically lied here. With statements that were untrue. e.g. 'When you walk, you are moving through the rain at a slower speed, which means that you are exposed to the rain for a shorter amount of time. When you run, you are moving through the rain at a faster speed, which means that you are exposed to the rain for a longer amount of time.'

If you're curious what Bard made of this puzzle...

Show/Hide Google's Bard AI's Answer

If you're curious what ChatGPT made of this puzzle...

Show/Hide ChatGPT's Answer