Answer to Puzzle #57: Making a Fair Decision With a Biased Coin
57. How can you use a biased coin to make an unbiased decision?
That is to say the coin does not give heads or tales with equal probability. How can you ensure that decisions made with the coin do have a 50:50 chance?
That is to say the coin does not give heads or tales with equal probability. How can you ensure that decisions made with the coin do have a 50:50 chance?
I went looking for this and found something more complicated than I could ever have expected. We're going to look at 3 different 'solutions':
 Before reading the answer can I interest you in a clue?
Before reading the answer can I interest you in a clue?Off the Wall
Just toss the coin as usual and don't worry about it being biased. Unless someone knows the bias then nobody is at a disadvantage. I'm thinking of a scenario where say you are deciding who gets the first kick in a football match. Granted some of the outcome is decided at the point where one of the teams elects for head or tails. But it's the same for both, neither team would be advantaged. This breaks down if you have to make more than one decision.The Obvious
The obvious thing to do is to use large numbers to establish the bias and eliminate it. So let's say we toss the coin 100 times and get 70 heads, 1000 times and get 701 heads, it becomes obvious that we know the bias and can design a game to bring the fairness back. In this case, for example rather than a single toss, the game might be to toss the coin 20 times and whomever picks heads would have to get 15 or more to win. This solution is fine. But it's not the best.The Clever
The reason I said this is more complicated than I could have expected is there are actual papers written on this. This solution was proposed by John von Neumann winner of the Fermi Award, member of the Manhattan Project. I wouldn't expect anyone to come up with the answer in an interview without serious prompting. On the other hand with prompting I think it's fairly easy.We are going to consider the possible outcomes of tossing the coin twice. Let's have p be the probability of a Head, q be the probability of Tails, where obviously q = 1 - p. The table below shows the probabilities for the possible outcomes for the double toss.
| Head | Tail | |
| Head | HH pp | TH qp |
| Tail | HT pq | TT qq |
And that is quite interesting. As pq = qp, the probability of tossing a Head followed by Tails is the same as that of throwing a Tails followed by Heads. And we have two outcomes that have equal probability but are distinguishable. The HH or TT outcomes are of no use to us and we must disregard them if this happens and start again. Von Neumann wrote it like this:
- Toss the coin twice.
- If the results match, start over, forgetting both results.
- If the results differ, use the first result, forgetting the second.
Expansion
There are other things we can work out about our system. For example the probability of finding a result in the first round with our system is P(result)=2pq or P(result)=2p(1-p) which is a function that looks like this: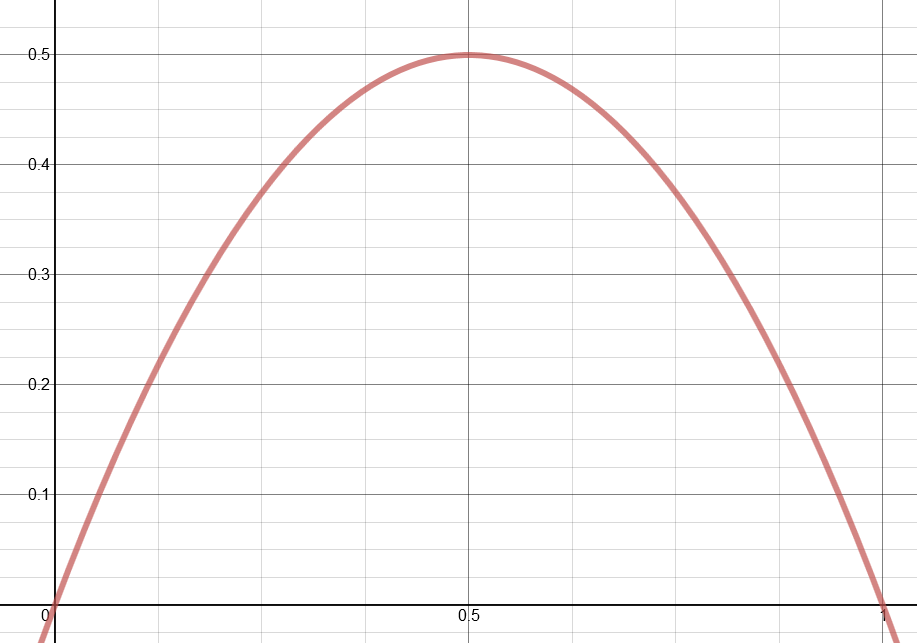
Which is to say that the more biased the coin, as in the further p (or q for that matter,) gets away from 0.5 the less likely we are to get a result. With an unbiased coin we only stand a 50/50 chance of getting a result using this method. Which makes sense as of the 4 outcomes from the double toss have equal probability, and only two of them are useful.
There's more to keep going with too. How about how many rounds we expect to have to play in order to produce a result? Let's call the expected number of rounds Er.
Er = P(result) + P(noresult) • (Er + 1)
Why? This is not unlike the two person duel puzzle we did as part of the truel puzzle. That is to say the expected number of rounds is one times the probability of getting it in the first round plus the probability of going on to the next round where we basically start again with one round higher. As in after a certain number of failed rounds the next round is no more or less likely to be a success.
Er = 2pq + (1 - 2pq) • (Er + 1)
Er = 2pq + Er + 1 - 2pqEr - 2pq
0 = 1 - 2pqEr
Er = 1 / 2pq = 1 / 2p(1-p)
Which unsurprisingly is just the reciprocal of the probability of success in the first round.
So the expected number of rounds is a function looking like this:
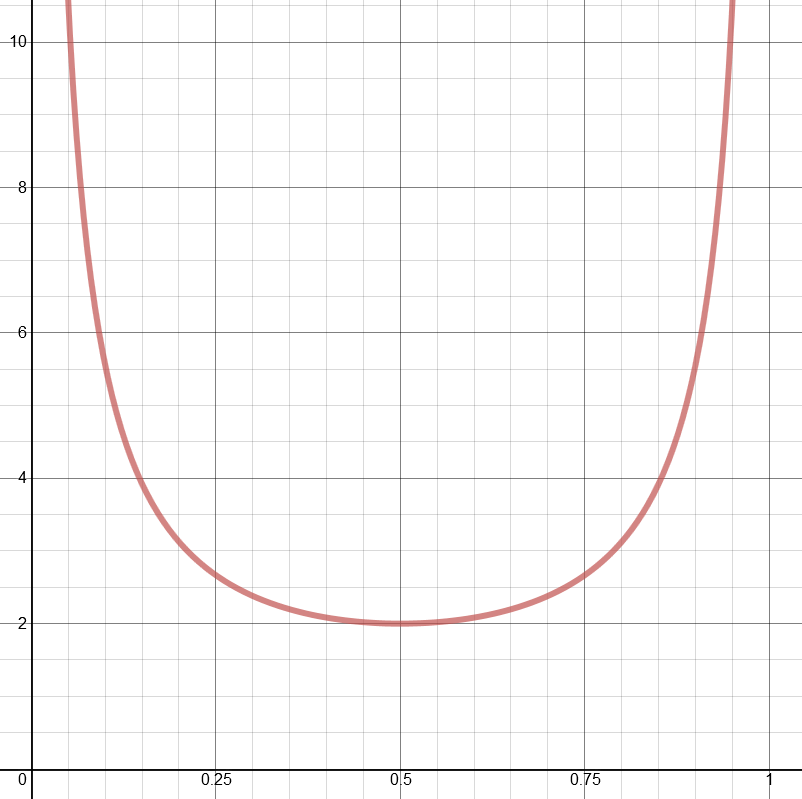
Obviously the expected number of coin tosses is simply twice the number of games, as we are tossing twice per game. You can see that as we move from unbiased (p = 0.5) the number of games required increases dramatically.
Further Work
Seriously, we're not done yet. Michael Mitzenmacher (Harvard algorithms bod,) in his paper Tossing a Biased Coin (PDF) takes things further. He looks at more tosses, for example if, for 4, HHTT could be looked at in a similar way to the von Neumann method. His objective is efficiency, reducing the total number of tosses required to produce a result. It's reasonably accessible, it's just beyond the scope of anything I'm prepared to go in to.Assumptions, After Thoughts
As I said I don't think it would be reasonable to expect someone to come out with all this lot in an interview. If someone does they've probably heard it before and are trying to style it out that they haven't. The way I would expect it to go in an interview would be to ask the question, listen whilst you think out loud, then ask you maybe what are the possible combinations of tossing it twice, what are the probabilities of each combination. Then nudge you in to noticing that two outcomes are different but have the same probability. Then maybe ask you if you can think of anything else interesting about the problem, or ask you to workout how long it would take to get a result or the likelihood of getting a result. And if you could find a more efficient way of doing it, but we have got pretty deep in to it by now.I think bard got it right, just didn't explain it very well.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.



