Answer to Riddle #67: How Far is the Horizon

67. How far is the Horizon?

This is not a typical 'Puzzle' but it is some common sense geometry. I saw some puzzles of the form 'John is stood on the beach...' I thought these all come down, basically, to working out the distance to the horizon. So let's just do that.

Diagram for calculating the distance of the horizon

Before reading the answer can I interest you in a clue?

There are a number of ways to make this calculation, the important thing is that you can justify any assumptions you make.

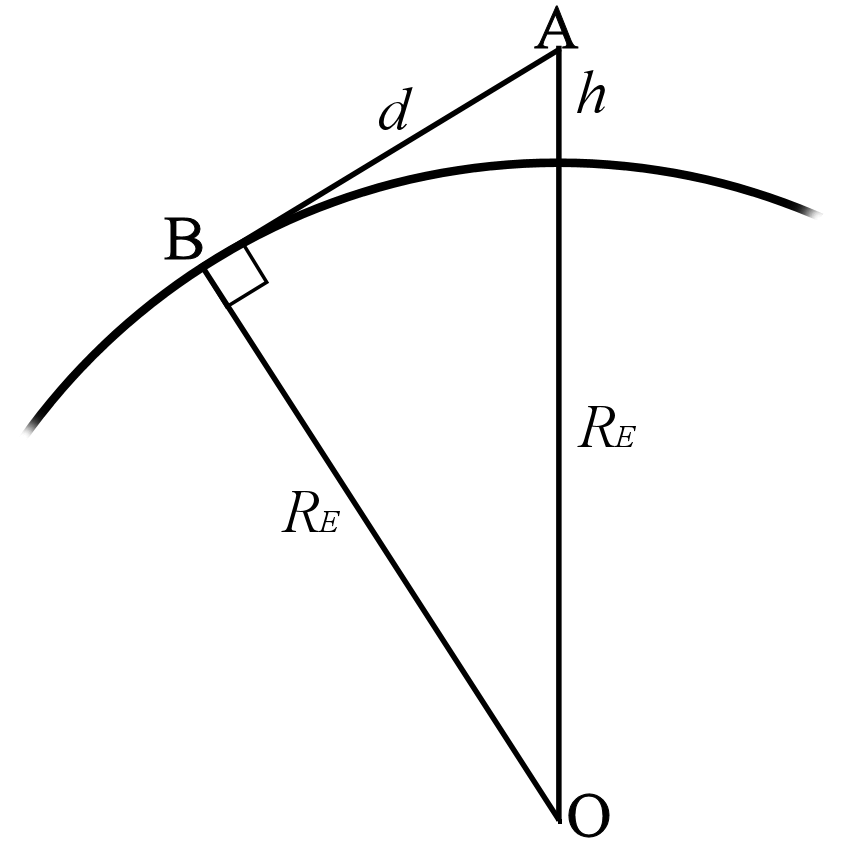
AOB is a right angel triangle where from O the opposite side 'd' is the distance to the horizon, the adjacent side 'R_E' is the radius of the earth and the hypotenuse is 'R_E' + 'h' where 'h' is the height of the observer. We will apply Pythagoras Theorem

X² + Y² = Z²
R_E² + d² = (R_E + h)²
R_E² + d² = R_E² + 2R_Eh + h²
d² = 2R_Eh + h²
d² = h(2R_E + h)
d = ±√h(2R_E + h)

The algebra to now should be fairly easy to follow. Note the ± is simply because in our 2D model the horizon is in both directions, not strictly necessary, but good for completeness.

On the right we have ±√h(2R_E + h) and we will be approximating this to √2hR_E. Some people would argue that the approximation is less accurate, but the earth is not a sphere, it's radius varies by ±15km and so using 2R_E + h seems like an accuracy we can't claim.

d = √2hR_E

Given R_E = 6,371,000m for me at least whose eyes are 6ft2 from the ground or 1.8796m the horizon is 4,894m away.

Two Objects Above Sea-level

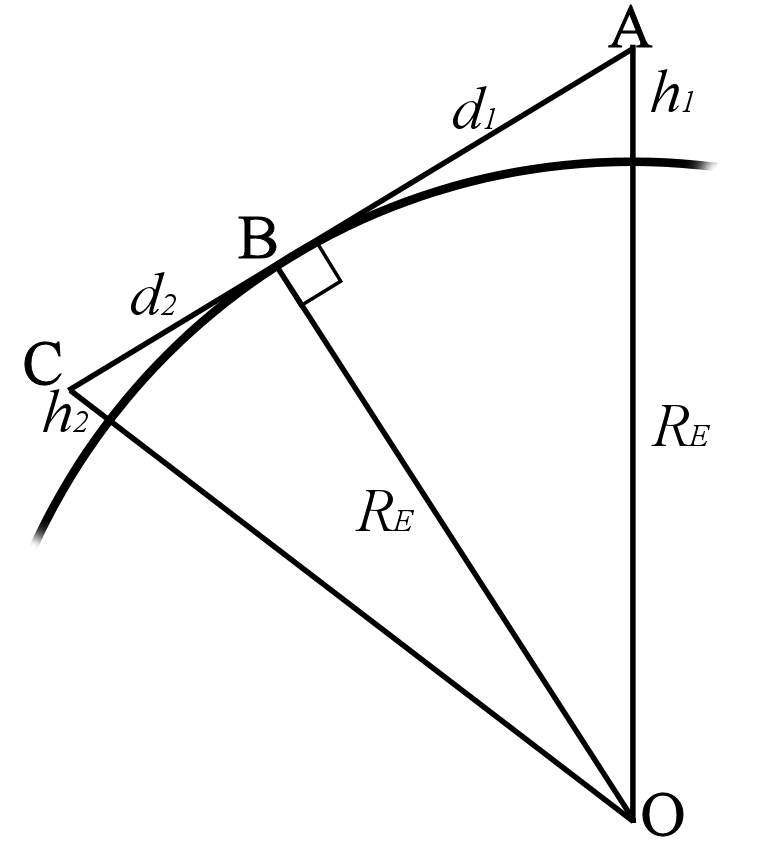Diagram for calculating the distance of the horizon when both parties are raised

So, to now, we have considered an observer for example stood on a beach looking at the horizon and calculating that distance. What if you have someone on the shore looking for the top of a ship's mast?

Since the limiting factor in how far we can see is the hump of the earth in the way as it just disappears ABC will be a straight line. We can simply add the tow horizon distances together. As in

d = d₁ + d₂ = √2h₁R_E + √2h₂R_E

As you would expect both AI's did well at this.

If you're curious what Bard made of this puzzle...

The distance to the horizon depends on your height above sea level. For a person of average height (5 feet 7 inches) standing at sea level, the horizon is about 3 miles away. If you are standing on a hill or tower, the horizon will be farther away. For example, if you are standing on a hill that is 100 feet high, the horizon will be about 12 miles away.

Here is a formula you can use to calculate the distance to the horizon in miles:

distance = 1.225 * sqrt(height)

where height is your height above sea level in feet.

For example, to calculate the distance to the horizon for a person of average height standing at sea level, you would use the following formula:

distance = 1.225 * sqrt(5 * 12)
distance = 3.1 miles

If you're curious what ChatGPT made of this puzzle...

Where next?
List of Puzzles Random Puzzle Next Puzzle

© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.

PayPal - The safer, easier way to pay online.

PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel

Answer to Riddle #67: How Far is the Horizon

Two Objects Above Sea-level

This Website Uses Cookies