Answer to Riddle #78: Secret Santa Maths
78. Secret Santa is a Western Christmas tradition in which members of a group or community are randomly assigned a person to whom they anonymously give a gift.
The rules for determining who buys for whom are as follows. All the participants put their names in a hat. Each player will draw a name in turn. If they should draw their own name they will return it to the hat and draw another. If the last person to draw draws their own name the game is void and everyone starts again. Otherwise people will not return the name to the hat and will buy a present for the person whose name they have drawn.
Adam, Bob and Carol are to play a game of Secret Santa. They will draw in alphabetical order. What are the odds that Adam buys for Carol?
The rules for determining who buys for whom are as follows. All the participants put their names in a hat. Each player will draw a name in turn. If they should draw their own name they will return it to the hat and draw another. If the last person to draw draws their own name the game is void and everyone starts again. Otherwise people will not return the name to the hat and will buy a present for the person whose name they have drawn.
Adam, Bob and Carol are to play a game of Secret Santa. They will draw in alphabetical order. What are the odds that Adam buys for Carol?
If you've not heard of Secret Santa, you may know it as Kris Kringel or 'amigo secreto', whatever you know it as the puzzler in you should know that the answer, however tempting, is not going to be a half:
Before reading the answer can I interest you in a clue?So it looks like the answer is 50/50, a half. The first move of the game is A pulling a name out the hat. If he pulls his own out he puts it back but other wise he has a 50/50 chance of picking B or C. So where's the problem.
We will cover the maths, but in principle the problem is this. If a chooses B or C the odds of the game completing successfully are not the same. Intuitively from the criteria for voiding the game 'If the last person to draw draws their own name the game is void and everyone starts again.' we can guess that this is more likely to happen if the last person, C, still has their name in the hat.
So lets work it out. In the diagram below we have 3 sections dealing with A, B and C's picks respectively. The notation is that 'AB' means A is buying for B. CA would mean C is buying for A.
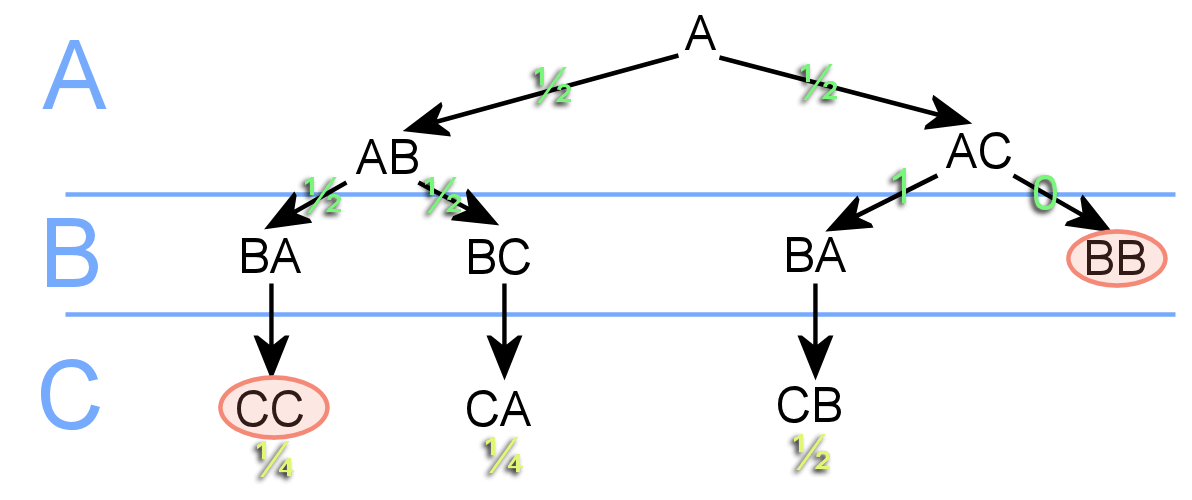Initially A draws B or C, effectively with a 50/50 chance as should he draw his own name he just puts it back. If he draws B represented by AB we are on the left hand side of the diagram. B can now draw A or C, (remember B has gone already,) represented by BA and BC respectively. If B draws A then on the path AB→BA then both A & B have gone leaving C with only C to pick, the game must be void. If A draws B the only viable path is AB→BC→CA
If A draws C represented by AC on the right hand side of the diagram. We move to B's turn, as C has already gone he can only pick A or B shown as BA or BB. He can not buy for himself and if he should pick his own name will return it to the hat. Effectively he has a 100% chance of picking A, as in BA. When C picks only B is left.
We can calculate the probability of each of the 3 outcomes, only two of which are valid by multiplying out the probabilities of each branch:
AB→BA→CC = ¼
AB→BC→CA = ¼
AC→BA→CB = ½
Of the games that are successful, we can renormalise, (that is to say eliminate the void game by dividing each result by ¾,) to say Adam buys for Carol two thirds of the time.
ChatGPT did the best on this one...
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
