Answer to Puzzle #3: The Fly in a Cubic Room
3. You are a bug sitting in one corner of a cubic room. You wish to walk (no flying) to the extreme opposite corner (the one farthest from you). Describe the shortest path that you can walk.
I worked this one out for myself so it clearly isn't that hard...
Before reading the answer can I interest you in a clue?
First consider the diagram:-
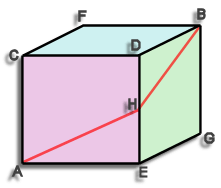
The problem phrased differently is that we have to get from point A to point B only moving along the walls.
The shortest route is shown it is A-H-B where H is the mid point of D-E.
The length of this route can easily be calculated, assume the cube has sides of length 1 unit (it doesn't matter what these units are, meters, feet, what ever) The distance A-H is the hypotenuse of a triangle 1 x ½ a quick bit of pythag tells us that A-H equals √(5/4). Similarly H-B has the same length hence the total length is 2 x √(5/4) this is actually equal to the square root of 5
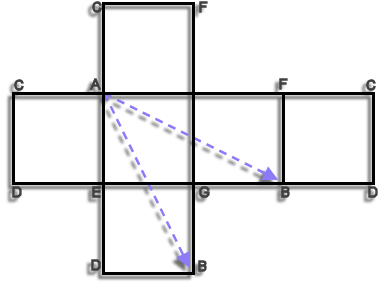
The above is a flat diagram of a cube net, such that you could cut it out and fold it to make the cube we have been considering, the labelling is the same. There are two point 'B's that when it is folded would become one. We know that the shortest distance between two points is a straight line so a rigorous mathematical proof is not necessary.
The diagram shows two acceptable routes but there are actually six. It's an interesting exercise to draw them all on to the cube net.
ETA: Some people have been confused by the diagram. I think possibly the line A-H looks like it might be the back edged of the cube, with H being the hidden corner. So we are absolutely clear I made a video, this time using Minecraft:
I genuinely can't tell if either got this right.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
First consider the diagram:-
The problem phrased differently is that we have to get from point A to point B only moving along the walls.
The shortest route is shown it is A-H-B where H is the mid point of D-E.
The length of this route can easily be calculated, assume the cube has sides of length 1 unit (it doesn't matter what these units are, meters, feet, what ever) The distance A-H is the hypotenuse of a triangle 1 x ½ a quick bit of pythag tells us that A-H equals √(5/4). Similarly H-B has the same length hence the total length is 2 x √(5/4) this is actually equal to the square root of 5
A-H-B = √5 = 2.236
A common wrong answer is to think the shortest route is A-C-B or A-E-B or A-F-B etc. (they are all the same) this has a length of 1 + √2 ie. about 2.414. For completeness I should say the distance without the restriction of having to stick to the sides is √3, about 1.732Proof this is the shortest route
So far we have calculated the shortest route, but not necessarily proved it to be so. Cameron Tiesma sent me this. Consider the following diagram:
The above is a flat diagram of a cube net, such that you could cut it out and fold it to make the cube we have been considering, the labelling is the same. There are two point 'B's that when it is folded would become one. We know that the shortest distance between two points is a straight line so a rigorous mathematical proof is not necessary.
The diagram shows two acceptable routes but there are actually six. It's an interesting exercise to draw them all on to the cube net.
ETA: Some people have been confused by the diagram. I think possibly the line A-H looks like it might be the back edged of the cube, with H being the hidden corner. So we are absolutely clear I made a video, this time using Minecraft:
To see the video you'll have to click here. The video will appear below, or to view it in YouTube you can click click here. Apologies for this nonsense, it's because you're on a mobile device and Google thinks this page is not mobile friendly if I embed YouTube videos using their own code.
I genuinely can't tell if either got this right.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
