Answer to Riddle #79: Flatland Airports

Before reading the answer can I interest you in a clue?

So what's going on? I'm hoping the diagram below will make things a little clearer:



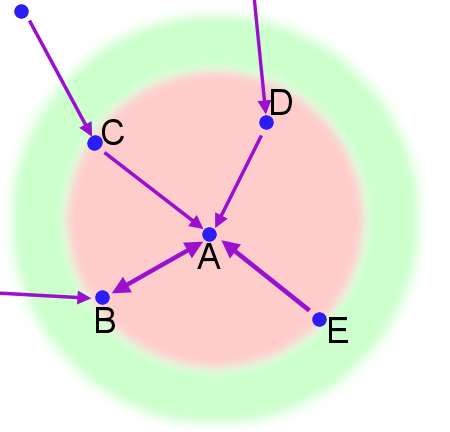
So the airports (blue dots,) are randomly sited on an infinite plane. Each airport has an aeroplane that will take off and land at the nearest neighbouring airport, (i.e. excluding the one it started at.) The map shows by means of a purple arrow the direction of travel for each aeroplane.

There are a few things we can start to notice: If there are two airports in isolation they will swap aeroplanes. If there are three airports isolated in a straight line the aeroplanes from the outer two will move to the middle, and the plane in the middle will move to whichever neighbour is nearest. In the bottom right there is an airport that has 3 arriving aeroplanes, and it's not hard to speculate that we could add a fourth arriving from the bottom right...

Why is it not infinity?

So lets call the airport at which we are trying to maximise the number of arriving aeroplanes 'A', it's neighbours will be 'B' 'C' 'D' etc. At some point, as we keep adding airports, they will be come each other's nearest neighbours and not 'A's

If that's not clear, look at the map above, consider the airport with three arrivals. As stated, it's pretty easy to see that we could add another airport to the bottom right that would also fly to 'A'. But if you were to keep adding them where would they be positioned in order that they fly to 'A' and also, importantly, not stop any of the aeroplanes at any of the other airports from flying to 'A'. If that's still not clear click here to read a little more.

The above diagram is the bottom right part of the map shown in the previous section, 'A' being the airport with 3 aeroplanes arriving 'B' 'C' & 'D', I've added the 4th arrival 'E.' The question is where would we add another airport 'F' such that there would be 5 aeroplanes travelling to 'A'? In the pink zone and it could be that 'F' would travel to 'A', but it would also have the effect of causing one of 'B' 'C' 'D' or 'E' to travel to it and not to 'A.' For the green zone and further out 'F' would definitely travel to one of the other airports. And if it were near enough it still may make one of 'B' 'C' 'D' or 'E' travel to it.

We will look at two airports 'A' & 'B' and calculate the possible positions for 'C' such that it goes to 'A' without preventing 'B' from going to 'A.'

Working out the limit

It seems clear that the way to maximise the number of arrivals is a sort of hub and spoke design. We put 'A' at the center and surround it with 'B' 'C' 'D' etc. The question is how many can we surround it with before they become closer to each other than they are to 'A.' Something along the lines of this... (Noting of course that the question is clear that no two of airports are exactly the same distance apart.)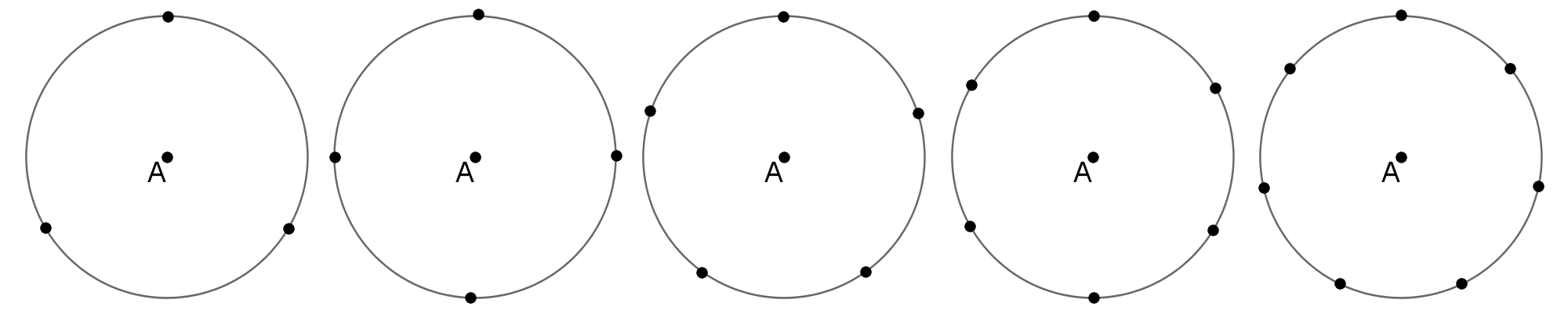



If it wasn't before the reason for the limit now becomes, as we add airports to the rim their separation becomes smaller.

Consider the airport an airport 'A' and it's nearest neighbour 'B.' We will then workout how close we can bring 'C' such that 'C' travels to 'A' without interfering with 'B.'
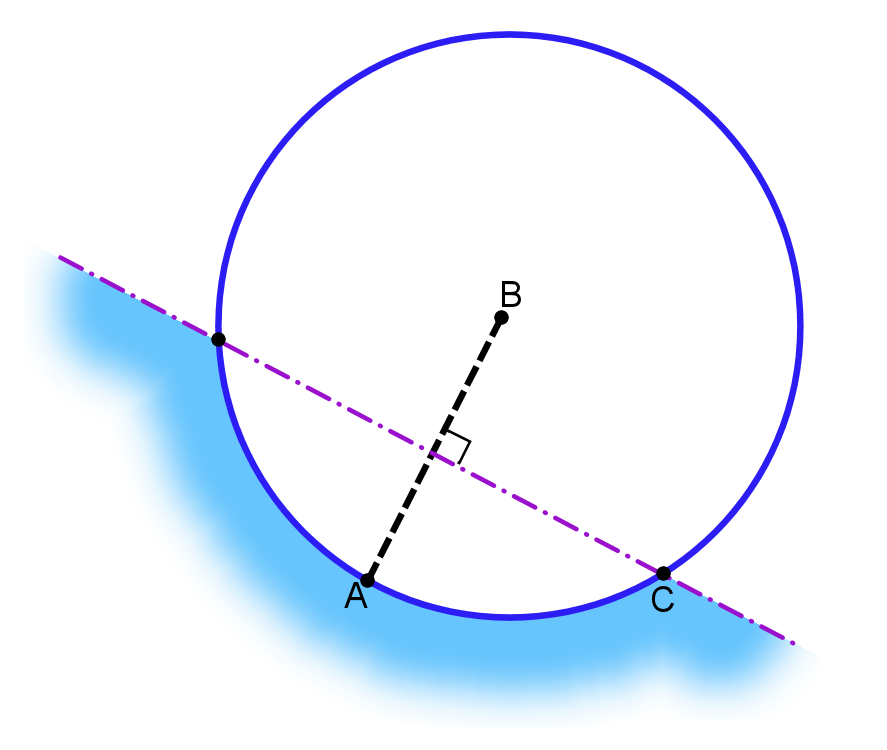
('A' is still the arriving airport.)

In order that 'C' travel to 'A' it must be on the 'A' side of the purple line. The purple line is the perpendicular bisector of the line 'AB' and anywhere on the 'A' side of it is nearer 'A' than 'B.'

Next we must ensure that 'B' still travels to 'A' and not to the newly introduced 'C.' If 'C' were inside the blue circle of radius 'AB' then 'B' would be nearer 'C' than 'A.'

Acceptable positions for 'C' are then in the light blue zone but we are trying to minimise the angle and that is with 'C' at the position shown.

'△ABC' form an equilateral triangle thus the angle 'BAC' is 60°. However, the question specifically excludes the possibility of any of the airports being the same distance apart. So the angle must be greater than 60°. Any amount greater, but it can not be ≤60° Thinking back to our spoke and wheel design, standing at 'A' the minimum angle between any two other points is >60°. Hence the maximum that can fit, and the answer to our question is five aeroplanes.



Both the AI's failed to solve this though ChatGPT got closest.

If you're curious what Bard made of this puzzle...

Show/Hide Google's Bard AI's Answer

If you're curious what ChatGPT made of this puzzle...

Show/Hide ChatGPT's Answer