Answer to Puzzle #37: An Aeroplane Takes a Round-trip in the Wind

Before reading the answer can I interest you in a clue?

Firstly by roundtrip we mean it starts in the same place it finishes. It's route is not important as it will be subject to a headwind and a tail wind or their components in equal amounts. We will consider the simplified case the plane flies directly in to the wind and turns around and heads straight back. Or vice versa.

Instinctively it feels like the two should exactly cancel out. But that is not the case.

Let's do a worked example. Lets say our plane has to travel 300 miles there and 300 miles back. It has a standard cruising speed of 600mph. In the case of no wind it will travel the 600 miles in 1 hour exactly. Simple enough.

Let us say that the wind speed is 100mph so the plane will be wind assisted to 700mph and slowed to 500mph
- Wind Assisted: 300 miles at 700mph takes 0.429 hours
- Wind Slowed: 300 miles at 500mph takes 0.6 hours
- Total Time: 1.029 hours

So the total time has increased. And that is the answer to the question. But what has happened? Why don't they cancel out? Well simply because the journey against the wind is slower and lasts longer the plane is against the wind for longer. And the converse is true.

There are a whole load of puzzles that work the same way as this relating to ships in the sea, internet download speeds and so on. You can imagine something like your internet service provider throttles your download speed by a couple of megabits at peak times and increases it by the same amount off peak. Which sounds fair unless you know.

A really obvious example might be 'Over a two mile journey I'm stuck in traffic for a mile and only manage to average 1mph, the traffic clears and I average 60mph for the last mile. What is my average speed?' About 30mph right? No. I have travelled 2 miles in 1hour and 1 minute. My average speed is less than 2mph. I call this category of puzzles: 'Things that last longer, on average, last longer.'

The General Solution

The algebra is as tedious as it is unsatisfying. Nonetheless it is written out below. Let T₀ be the time without wind. T_W be the time with wind. V the unaided speed. W the wind speed, so it flies one way at V+W and V-W the other. Let D be the distance there and back. T₀ trivially is given by: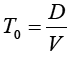



T_W is given by using the two trips of D/2 at speeds V+W and V-W



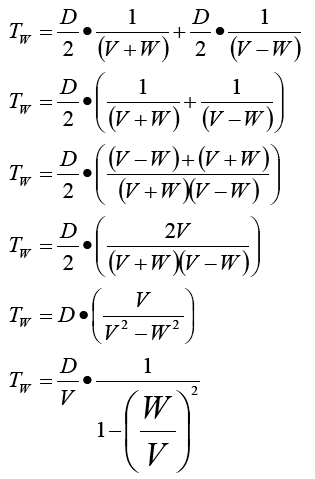
The purpose of such a bizarre arrangement will become clear when we show T₀ over T_W



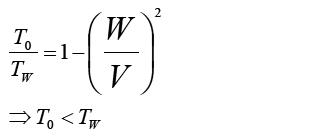
for all non zero values of W

Something hidden in the maths that may not be apparent is since W is squared it doesn't matter whether the wind direction is positive or negative. Not that we were exactly rigerous in our sign convention.

In The Limit

In question 33 we looked at the concept of 'in the limit.' The process of trying to understand our model by taking one of the variables to the extreme. In this case I would like to consider what happens if the wind speed is very nearly, or tends towards, the same as the plane's cruising speed.

The part of the journey with a tail wind would be twice as fast. But the part with the head wind would never, or would almost never, be completed.



I give Google and Bard 8/10 for this, ChatGPT 2/10.

If you're curious what Bard made of this puzzle...

Show/Hide Google's Bard AI's Answer

If you're curious what ChatGPT made of this puzzle...

Show/Hide ChatGPT's Answer