Answer to puzzle question #13: Circular Field, Hungry Dog
13. You are standing at the centre of a circular field of radius R. The field has a low wire fence around it. Attached to the wire fence (and restricted to running around the perimeter) is a large, sharp-fanged, hungry dog. You can run at speed v, while the dog can run four times as fast. What is your running strategy to escape the field?
I really like this one, at first I thought it wasn't possible, we'll go through one of the ways that doesn't work...
Before reading the answer can I interest you in a clue?
Consider the diagram below:
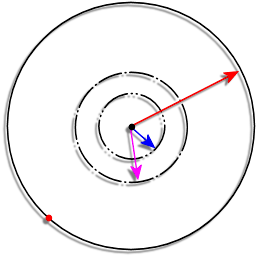
The strategy is to run in a circle of 0.2146R < radius < 0.25R until the dog is on the opposite side then make for the fence like the clappers.
I like this one.
Neither AI covered themselves in glory on this one.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
Consider the diagram below:

R - is the radius of the circle
X1 - is the radius of the inner dotted circle
X2 - is the radius of the outer dotted circle
R/v > πR/(4v)
So clearly we need to be closer to the edge than just in the middle, let us work out how far away from the centre we have to be in order that we have the advantage over the dog. Let our distance from the centre be xR where x is a number less than one eg. if R were 10m and we were 1.5m from the centre then x=0.15 Assuming that we can get the dog on the opposite side of the circle to us (I'll come back to that,) then the distance we must run is (1 - x)R where as the dog must always run πR we can equate the time associated with these distances, remembering the dog runs at 4v.(1 - x)R/v = πR/(4v)
x = 0.2146
The strategy is to run in a circle of 0.2146R < radius < 0.25R until the dog is on the opposite side then make for the fence like the clappers.
Other Possibilites
It seems possible that there are other solutions. Such as a spiral giving an angular component to your velocity. This would not work if your direction of travel was always away from the dog, (as in Θdog + π,) which was my first thought because at some point all your velocity would be angular. We could assume the dog would always move so as it would always run to try to match Θhuman. This seems solvable. You would need to consider that your radial velocity would be less than V because there is a tangental component. You could model with different angular velocities.Alternate versions
I've seen this written with a duck on a round lake, surrounded by a forest. At the edge of the lake is some kind of monster that can't swim. I suppose that makes sense as to why the monster can't get on the lake. But can't ducks fly?I like this one.
Neither AI covered themselves in glory on this one.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.



