Answer to Riddle #68: Arrangements of Red & Blue Marbles
68. You have 50 red marbles and 50 blue marbles, other wise identical. You have 2 identical jars. A marble will be selected at random, from a jar selected at random. How would you apportion the marbles so as to maximise the chances of a red marble being selected?
Can you prove it?
Can you prove it?
Interesting puzzle this. For a while I thought there is just no way. But there is, let's take a look.
Before reading the answer can I interest you in a clue?We're assuming that the selection of the jars is beyond our control. Whomever selects will decide on which jar with a 50 50 distribution. All we can work with is the marbles in the jars.
A formula for working out the probability of picking a red is not so hard to derive. It's going to be .5 times the probability of picking a red from the first jar + .5 times the probability of picking a red from the second jar. And the probability of picking a red marble from any jar is the number of red marbles in the jar over the total number of marbles in the jar. (Note it doesn't say there has to be 50 marbles in each jar!)...
P(R) = .5R1 / (R1 + B1) + .5R2 / (R2 + B2)
If we could get one of the jars up to 100% red without dropping the percentage red in the other jar too far. At this stage I can tell you that the optimal arrangement is to put one red marble in one jar and all the other marbles into the other jar. Plug in the numbers and we get...
P(R) = .5 * 1 + .5 * 49 / 99 = 0.747474
What we have done is ensured that if the first jar is picked there is a 100% chance of picking a red marble, whilst diluting the presence of blue marbles in the second jar as best we can.
Proof
I'm using the phrase loosely here, rather than a proof it's more of a demonstration. One way of showing that a function is at a maxima is to show that any move away from that point reduces the function's value. Not proof that it is the maximum but a maxima. Since the problem is not really defined for no marbles in one of the jars the only moves we have are to add to the first jar either a red or a blue marble. For those positions the probabilities fall to 0.745 and 0.5 respectively. So we're on track.Next we have the equation P(R) = .5R1 / (R1 + B1) + .5R2 / (R2 + B2) but actually not all the variables are independent. There are only 50 of each marble so R2 = 50 - R1 and similarly B2 = 50 - B1. This gives us an equation with only two variables...
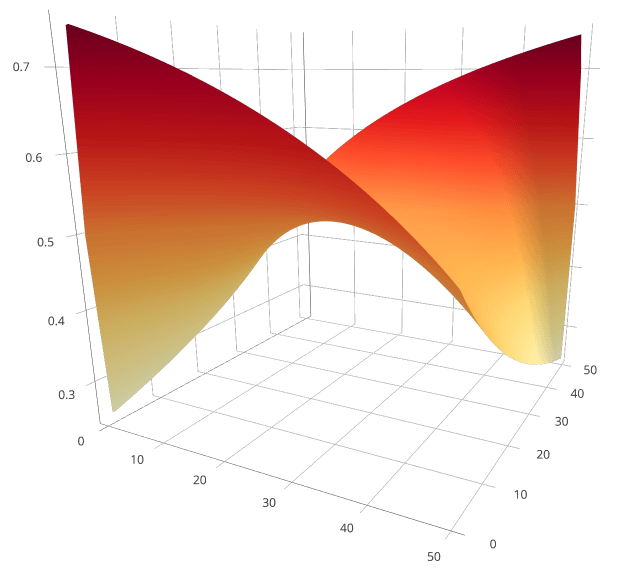
P(R) = .5R1 / (R1 + B1) + .5(50 - R1) / (100 - R1 - B1)
Which is a help because we can graph it as I've done above. You can interact with the graph or technically a 3D surface plot at plot.ly the R1 axis is on the left the B1 on the right. Note the symmetry as we move from one red marble in jar one to one red marble in jar two. Also that the maxima is right by the minima, this is the reversal of the optimal strategy i.e. putting one blue marble in the jar that had one red marble in it.
Assumptions
I'm assuming that you have to use all the marbles. If you read the question differently then you could only use one colour, put the rest in your pocket. I'm pretty confident my answer is the one that an interviewer would be looking for.Google's Bard AI had no problem with this puzzle ChatGPT on the other hand...
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
