Answer to Riddle #73: Square root of 12345678987654321?
73. What is the square root of 12345678987654321?
Square roots are impossible to work out, right? Well they're certainly very difficult but this is a puzzle not a maths test, so there must be something we can do:
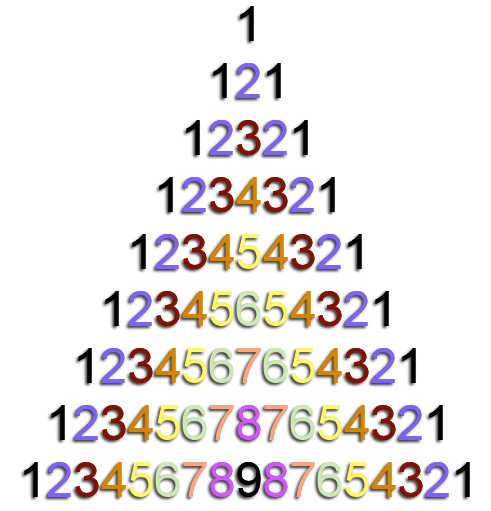 Before reading the answer can I interest you in a clue?
Before reading the answer can I interest you in a clue?The clue I gave you was to consider the square root of 121. √121 is, as we all know, 11. I think together with the number pyramid that's quite a clue. But before we get on to that lets look at something else.
The number 12345678987654321 might more usually be written 12,345,678,987,654,321 or roughly a bit more than 1016. This is a useful ballpark because 10 to the power of even numbers are easy. √100 = 10. √10,000 = 100. √1,000,000 = 1,000 and so forth. We know that our answer is going to be in the order of something a little bit bigger than 108 or 1xx,xxx,xxx. The question is how much bigger.
Back to 112
√121 = 11. Lets take it a bit further. Let's look at 1112, that is the last sum you will have to do. If you actually work it out long hand the pattern should be more obvious. It's 12321.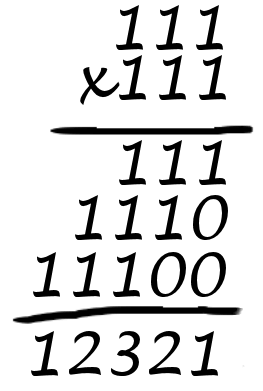
Hopefully by now you can see the pattern and why. 11112 = 1234321 and so on. The pattern being, from a purely non mathematical perspective, that the highest number, the one in the middle of the sequence such as 1234321 is the number of 1's in the square root. The square root of 12345678987654321 is 111,111,111
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.



