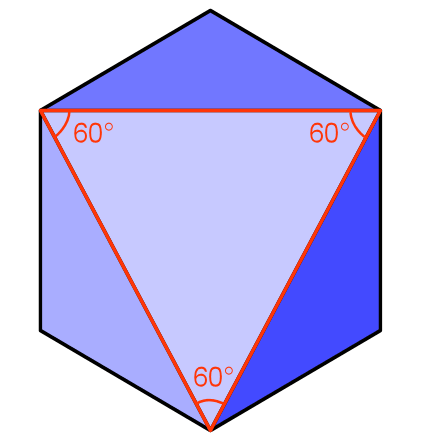
Answer to Puzzle #44: Diagonals on the Face of a Cube. What's the Angle?
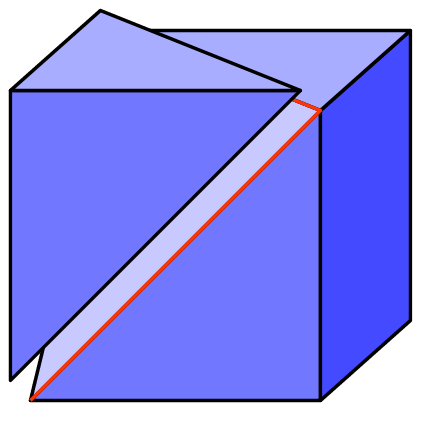
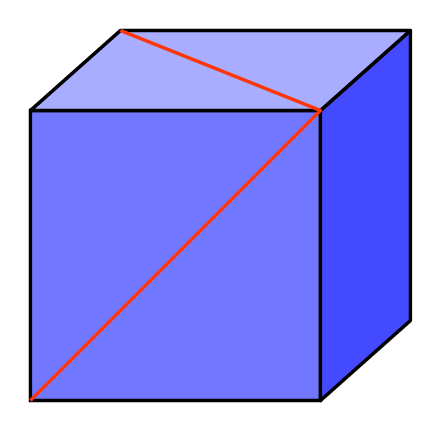44. The two red lines in the diagram shown are drawn diagonally on the faces of a cube. What is the angle between them at the point where they join?
I got this puzzle from an article on BBC news called 'Martin Gardner, puzzle master extraordinaire.' More spacial reasoning than a puzzle in the conventional sense but let's take a look.
Before reading the answer can I interest you in a clue?
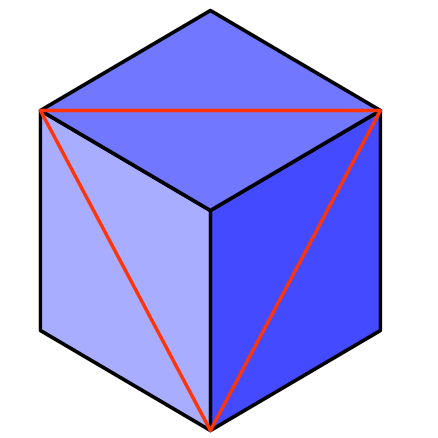
It might be that if you are in a particularly mathematical frame of mind you are trying to use a three dimensional co-ordinate system and a matrix transform to project the 45° angles in the corners in to a different plane. By all means. But it's not necessary, essentially this is a 2D problem, it's just about finding the right two dimensions to work in. Let's add another line to the diagram and see how we go.
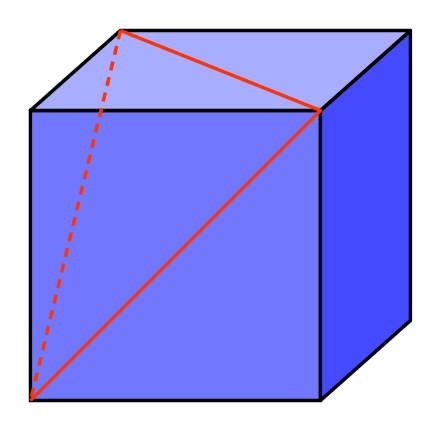
Any clearer? The dotted line completes a triangle. What's more since all it's edges are made up of diagonals from the squares, they are all the same length, it is an equilateral triangle. Like all equilateral triangles it's internal angles are each 60°
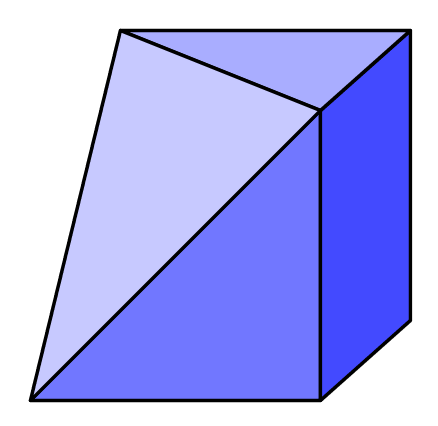
A problem I have found with these 3D nets is not everyone sees them the same, it's like an optical illusion. So at some point over the next few images it should become clear what I'm driving at...
And finally, just because we can.
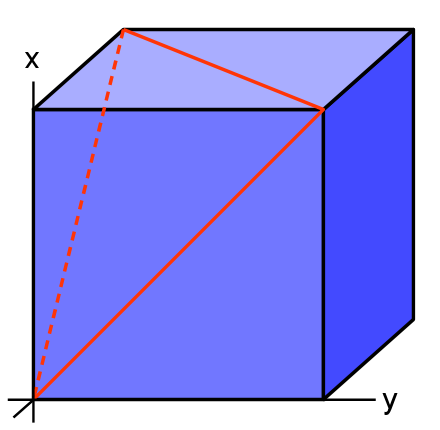
The above diagram shows a standard right handed co-ordinate system with the label on the z axis hidden. We will calculate the angle of the two red lines that meet at the origin. The first being defined as (1,1,0) and the second (1,0,1)
The angle between to vectors is given by:
cos θ = (u•v) / (|u||v|)
cos θ = (1•1 + 1•0 + 0•1) / (√2√2)
cos θ = 1/2
⇒ θ = π/3 or 60°
It might be that if you are in a particularly mathematical frame of mind you are trying to use a three dimensional co-ordinate system and a matrix transform to project the 45° angles in the corners in to a different plane. By all means. But it's not necessary, essentially this is a 2D problem, it's just about finding the right two dimensions to work in. Let's add another line to the diagram and see how we go.
Any clearer? The dotted line completes a triangle. What's more since all it's edges are made up of diagonals from the squares, they are all the same length, it is an equilateral triangle. Like all equilateral triangles it's internal angles are each 60°
A problem I have found with these 3D nets is not everyone sees them the same, it's like an optical illusion. So at some point over the next few images it should become clear what I'm driving at...
And finally, just because we can.
Vector Maths
As I've said before it's my intention that anyone using this site does not need formal maths training. But where there is an obvious maths solution I will try to include it.The above diagram shows a standard right handed co-ordinate system with the label on the z axis hidden. We will calculate the angle of the two red lines that meet at the origin. The first being defined as (1,1,0) and the second (1,0,1)
The angle between to vectors is given by:
cos θ = (u•v) / (|u||v|)
cos θ = (1•1 + 1•0 + 0•1) / (√2√2)
cos θ = 1/2
⇒ θ = π/3 or 60°
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
