Answer to Puzzle #40: 4 & 7 minute hourglasses to measure 9 minutes
40. Using only a 4 minute and 7 minute hourglass or egg timer how would you measure exactly 9 minutes?
This puzzle comes to me via the same source as the previous four. It also apparently appears in a book called 'Are You Smart Enough to Work at Google?'
Before reading the answer can I interest you in a clue?The puzzle appears quite difficult. It's not dissimilar to the 'Die Hard Water Puzzle' but it is somewhat more complicated. Before we can take a run at it we're going to have to build some tools, we will then use them in combination.
Addition
The simplest of our tools. We can combine hourglasses in series. We could use the 4 and the 7 one after the other to measure 11 minutes. Or any other simple combination.Difference
If we were to start both hourglasses together, flip the 4 when it reaches the end the difference between it ending for the second time and the 7 minute ending is 1 minute. The difference between 4 runs of the 4 and 3 runs of the 7 would be 16 as against 21 respectively. So 5 minutes.Early flipping
We could for example start both timers together. When the 4 minute hourglass runs out we know that the 7 minute hourglass has run for 4 minutes also and so must have 4 minutes of sand in the bottom. If we flip it now it will necessarily run for 4 minutes.Bringing it together
We already have a solution. It's most of the way there in the 'Difference' section above. We said if we start them both together and flip the 4 minute hourglass every time it runs out the difference between the 7 minute hourglass ending and the and the 4 minute hourglass ending for the second time is 1 minute. We just then need to flip it two more times to get 9 minutes. As shown:
Clearly though a better solution would be one that didn't require us to wait 7 minutes before we start. And there is a solution that allows this. We need to add 2 minutes on to the end of the 7 minute hourglass. Since the twice-flipped 4 minute hourglass will stop at 8 minutes we can flip our 7 minute hour glass here for the second time. At this point it will have been running for 1 minute, we will flip 1 minute's worth of sand back to the top and it will run for another 1 minute. This will total 9 minutes. As shown:
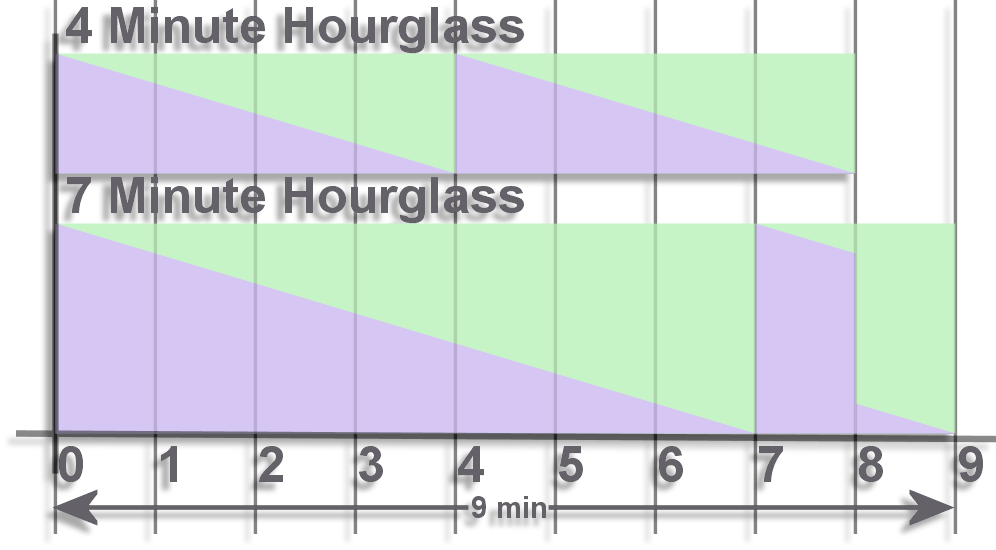
Not sure how to rate this for difficulty. When you have the solution in front of you it's almost trivial. But prior to that it seems very hard.
Personally I don't think the AI's explained this as succinctly as I did.
If you're curious what Bard made of this puzzle...
If you're curious what ChatGPT made of this puzzle...
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
