Answer to Puzzle #53: The train, the Station and the Bee.

Before reading the answer can I interest you in a clue?

Firstly some preamble. Don't let the meters per second, arbitrary units, unsettle if you are not used to working metric. Call them miles per hour if it suits. Secondly interview type questions are very rarely going to be testing your maths or your physics directly, there are other ways of demonstrating that. Probably the more maths you have done the more complicated you are making this in your head imagining summing some kind of geometric series of shortening Bee flights. Not necessary. These puzzles are designed to test the way you think not your maths.

We have the speed of the Bee and we can easily determine the total travel time from the uniform deceleration of the train. Using s=(u+v)t/2 the time the train spends in the station is 20 seconds. For more on how this is determined click here to display a paragraph on simple equations of motion.

There 4 equations concerning bodies in motion that are very useful. using the variables u = initial velocity, v = final velocity, t = time, a = acceleration & s = distance travelled, they are also sign specific so for example if something is initially going upwards and u is positive then the acceleration due to gravity downwards would be negative.
The equations are as follows:

v = u + at
s = (u + v)t/2
s = ut + ½at²
v² = u² + 2as

Half of mechanics is just writing those equations down and trying to work out which variables you already know and which you want to know. Some of the equations are straight forward. v = u + at is almost true by definition if you start at 100m/s and accelerate at 10m/s² for 5 seconds you are going to be doing 150m/s. Obviously(?)

We are using s = (u + v)t/2. It's not a huge leap from s = ut, the most basic equation of motion, as in distance = speeds x time. Except (u + v)/2 is the average of the initial and final speeds. So 500=(50 + 0)t/2.

t = 20 seconds

In 20 seconds the Bee travels 800m

I think in terms of interviews that is probably about where it ends. Realising you don't have to sum an infinite series is the main thing. The rest is algebra heavy, probably too so to be asked in an interview. It doesn't mean though that you couldn't be asked how you might go about it.

Time of First Collision

Let's take a closer look at what's going on. The following graph is position up the Y axis and time along the X axis.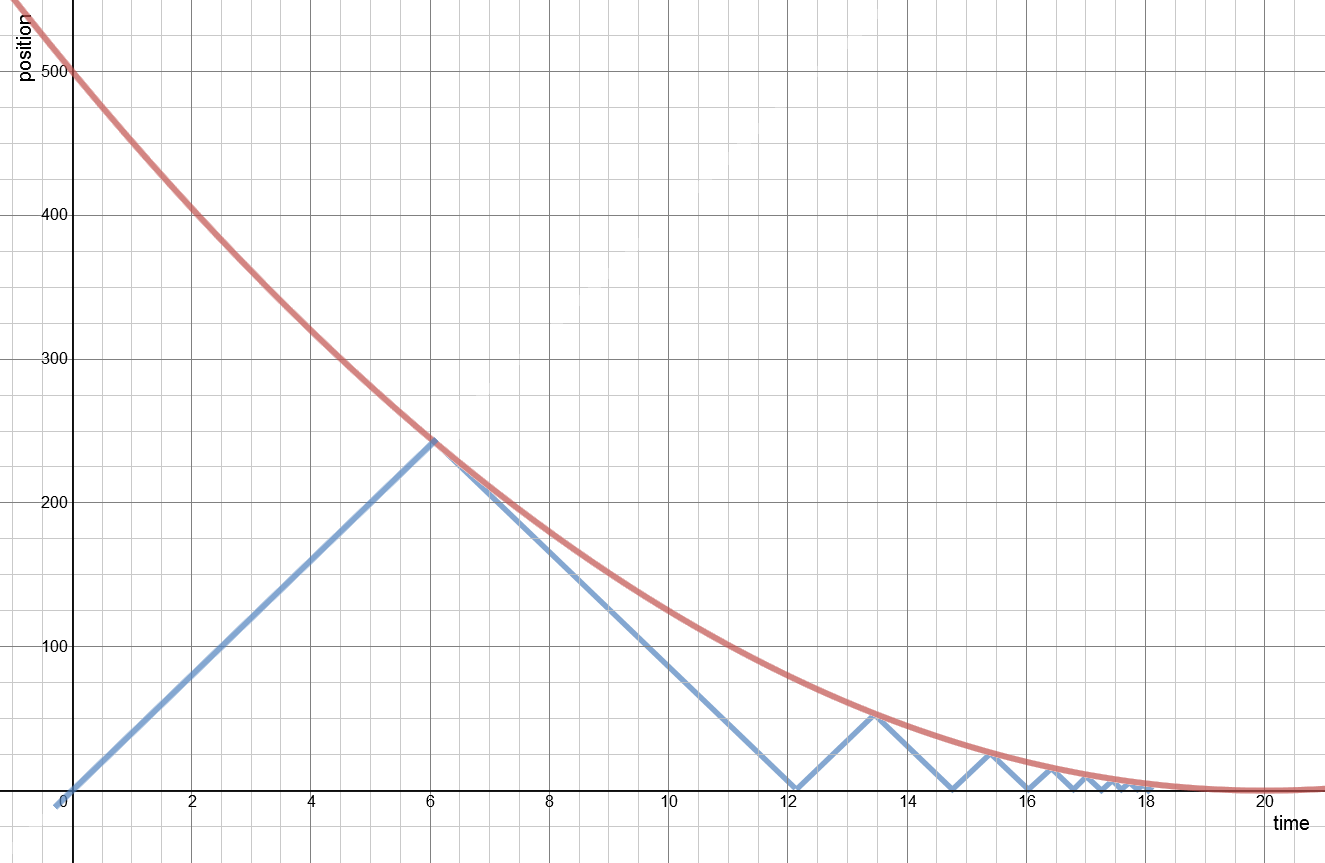



We can see there is a collision around 6 seconds that happens half way along the platform and this is what we will solve for. Using the strict sign convention of the buffers being 0 position and away from them is positive we have our setup. The maths is a bit messy.

v_T0 = -50m/s
a_T = 2.5m/s² (from above)
v_B = 40m/s
Position of the Bee = s_B = v_Bt = 40t
Position of the train = s_T = s_T0 + v_T0t + ½a_Tt² = 500 - 50t + 1.25t²

We are interested in when s_B = s_T so we put the two together and end up with a quadratic that looks likes
s = (90 ± √5600)/2.5 = 36 ± 29.933259 = 6.06674s

The significance of the other solution: Our model had the bee continuing, it didn't turn round, secondly the train was accelerating in a positive direction at a constant rate, it would not have stopped, it would have reversed it's path and continued to gain speed. As shown the train and the Bee would have met again at 2637m or 65.93s

Further Extension

My thinking was this. Can we be sure that when the Bee reaches the train and turns around, flying in the same direction as the train that the Bee will be able to fly faster than the train is currently travelling. I thought this might be interesting because, the faster the Bee is travelling the further down the track it will be when it meets the train and therefore the faster the train will be going. Conversely the slower the Bee flies the slower the train will be going at that point where it meets the train. So modelling this might be interesting. I had some help with this from the people over at stack exchange.

Firstly let's just check that our Bee will be OK. From the graph the gradients of the position, ie the velocity, look similar. That the point where they meet the Bee is travelling faster than the train. Keeping to our sign convention and origin we know v_T = -50 + a_Tt, where a_T = 2.5m/s², this gives us the train moving at -34.833m/s at the point where they meet for the first time. So the Bee will indeed be able to out run it.

But at what speed would it not? Some equations we have already:
1) v_T = -50 + (5/2)t
2) s_T = -50t + (5/4)t² + 500
3) s_B = v_Bt

Now at the point we are interested in the front of the train and the Bee are in the same place on the track, as in s_B = s_T. So
v_Bt = -50t + (5/4)t² + 500

Which is essentially the equation for collision time we solved above. Now however we are interested in the point when the Bee is just able to escape. As in v_B = - v_T, so we can substitute in equation 1.

-(-50 + (5/2)t)t = -50t + (5/4)t² + 500
50t - (5/2)t² = -50t + (5/4)t² + 500
(15/4)t² - 100t + 500 = 0

which solves to give t = 0 and t = 20/3

The significance of the t = 0 solution is that if the fly has zero velocity then they will meet at the buffers where the train will have zero speed. The intersting solution is t = 20/3. The speed associated with this time is 33⅓m/s and that is the minimum speed the Bee needs to be able to travel in order that it can survive.

Assumptions

As always with this kind of puzzle the assumptions are based around the fact that the train and the Bee are just analogues for idealised particles. So it's really anything you can think of to do with that. Such as the Bee turns instantly, (obviously defying the laws of physics,) has zero size, that sort of thing.



Both AI's got this puzzle wrong. Differently wrong, but wrong nonetheless.

If you're curious what Bard made of this puzzle...

Show/Hide Google's Bard AI's Answer

If you're curious what ChatGPT made of this puzzle...

Show/Hide ChatGPT's Answer