Hint to Puzzle #55: Free Theatre Tickets for the First Person With a Birthday the Same as Someone in Front of Them in the Queue
55. There is a long line of people waiting outside a theatre to buy tickets. The theatre owner comes out and announces that the first person to have a birthday same as someone standing anywhere before him in the line gets a free ticket. Where will you stand to maximize your chance?
The solution to this problem relies on an understanding of the Birthday Paradox, that problem asks how large a group of people one would need in order that it becomes likely that 2 of them have their birthday on the same day (of the year.) In the answer we derive this as shown below, by looking at the results you may be able to answer the main question. There's an extra clue at the end.
The Birthday Paradox
We will be working with the probability that people do not have the same birthday. Why? The first person can't have the same birthday as anyone less by themselves, so lets look at the second person. At the point where we add the second person there is a 364/365 chance of them not sharing a birthday with the previous person. When we add the 3rd person there is there is a 363/365 chance of them not sharing a birthday and so on such that the nth person when added has a probability of not forming a share of (365 -n +1)/365. We can multiply these together to p(n') where that is the probability of, after n people we do not have a pair. n! is n factorial.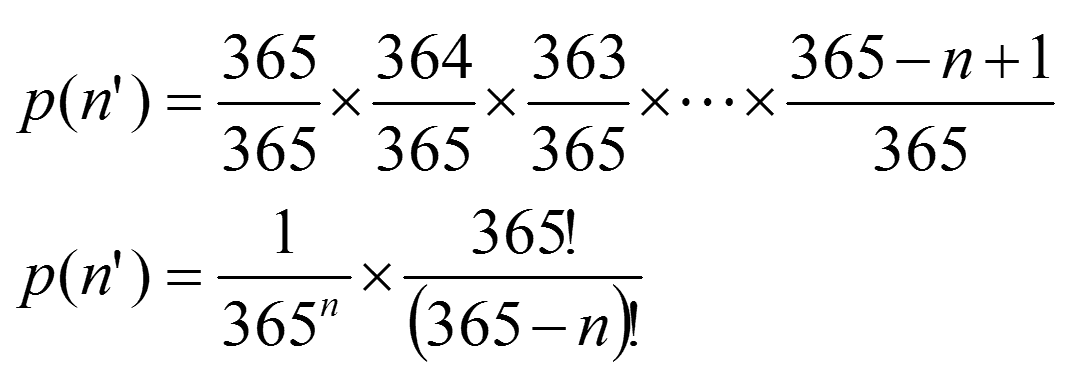
It's probably worth some exposition as to how we make the step... 100 x 99 x 98 x 97 x 96 x 95 x 94 x 93 x 92 x 91 = 100!/90!Which is a perfectly good equation for p(n') or 1 - p(n) save one thing. 365! is roughly equal to 2.51x10778 and so it's difficult to calculate so we must re arrange a little p(n') = 365Pn/365n where P indicates the Permutation function. The permutation function is defined exactly as we are using it, 365Pn is defined as 365!/(365-n)!. We're using this simply because we can calculate it, there is a button on a calculator and a function PERMUT(365,n) we can use in spreadsheet.
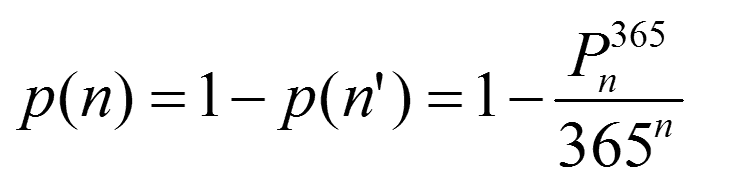If you punch in the number 23 you get a value of 0.507297234, this is the first time p(n) is greater than 0.5 and hence the reason why the answer to the birthday paradox is 23. The distribution is shown in the graph below.For an extra clue, if you're sure, click here
Where next?
Questions Answer
© Nigel Coldwell 2004 - – The questions on this site may be reproduced without further permission, I do not claim copyright over them. The answers are mine and may not be reproduced without my expressed prior consent. Please inquire using the link at the top of the page. Secure version of this page.
PayPal
I always think it's arrogant to add a donate button, but it has been requested. If I help you get a job though, you could buy me a pint! - nigel
